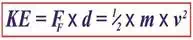Combining Kinetic Energy Formulas to Calculate
Velocity
|
As an
engineer, I often use the fact that formulas share a single common factor in
order to set them equal to each other, which enables me to solve for a
variable contained within one of them. Using this approach
we’ll calculate the velocity, or speed, at which the broken bit of ceramic
from the coffee mug we’ve been following slides across the floor until it’s
finally brought to a stop by friction between it and the
floor. We’ll do so by combining two equations which each
solve for kinetic energy in their own way. Last
time we used this formula to calculate the kinetic energy, KE, contained
within the piece, KE =
FF ×
d (1) and we
found that it stopped its movement across the floor when it had traveled a distance, d, of 2 meters. We
also solved for the frictional force, FF, which hampered its free
travel, and found that quantity to be 0.35 kilogram-meters/second2. Thus
the kinetic energy contained within that piece was calculated to be 0.70
kilogram-meters2/second2. Now
we’ll put a second equation into play. It, too, provides a
way to solve for kinetic energy, but using different
variables. It’s the version of the formula that contains the
variable we seek to calculate, v, for velocity. If you’ll
recall from a previous Topic, that equation is, KE =
½ × m × v2 (2) Of
the variables present in this formula, we know the mass, m, of the piece is
equal to 0.09 kilograms. Knowing this quantity and the value
derived for KE from formula (1), we’ll substitute known values into formula
(2) and solve for v, the velocity, or traveling speed, of the piece at the
beginning of its slide. Combining
Kinetic Energy Formulas to Calculate Velocity The
ceramic piece’s velocity is thus calculated to be, KE =
½ × m × v2 0.70
kilogram-meters2/second2= ½ × (0.09
kilograms) × v2 now
we’ll use algebra to rearrange things and isolate v to solve for it, v2 =
2 × (0.70 kilogram-meters2/second2) ÷ (0.09 kilograms) v =
3.94 meters/second =12.92 feet/second = 8.81 miles per hour |