Computing Potential Energy

Previous Topic we discovered that objects acquire potential energy as it relates to gravity based on the height those objects are elevated above the ground.   We also introduced an equation to calculate the potential energy of a coffee mug perched on a shelf.   We’ll work with that equation today and compute the latent energy that’s hidden within that mug.

Here again is the equation to determine potential energy, put in terms relating to gravity,

PE_{gravitational} = m × g × h

where m is the mass of the mug, h is the height it’s been elevated above the floor, and g is the Earth’s acceleration of gravity factor, as explained in a previous Topic, Sir Isaac Newton and the Acceleration of Gravity.

 The equation above can be solved using either English or metric units.   In the US it’s generally standard practice to perform calculations using English units, such as feet and pounds.   But when measuring mass a less familiar English unit, the slug, comes into play.   If you’re interested in learning more about this unit, go to a previous Topic entitled, The Force of Gravity.

 The kilogram is the metric equivalent of a slug.   Since it’s the unit of mass most commonly used throughout the world, we’ll use it to perform our calculation.

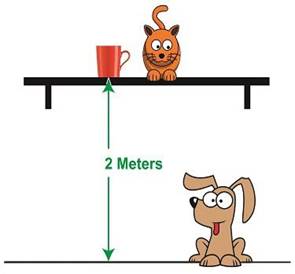
Let’s say our mug has a mass of 0.25 kilograms, the shelf it’s resting on is 2 meters above the floor, and g is 9.8 meters/second².   The mug’s gravitational potential energy would then be expressed as,

PE_{gravitational} = (0.25 kg) × (9.8 meters/second²) × (2 meters)

PE_{gravitational} = 4.9 kg • meter²/second²

      Next topic we’ll expand on our discussion of potential energy and discuss the Law behind the phenomenon and the fact that energy can only be converted from one form to another.