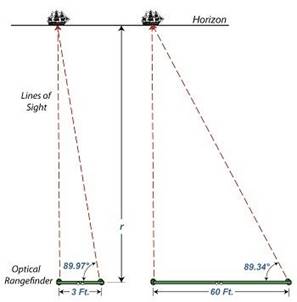
Optical Rangefinders, Why Bigger is Better

 Last time we discussed the fact that ultra fine gradations must be applied to a rangefinder’s indicator gauge in order to make accurate measurements of extremely long distances.    Today we’ll see how using a bigger rangefinder effectively solves this problem.

Figure 1 illustrates the subject.   The left side shows what happens when attempting to use a small rangefinder to measure the distance to that distant ship on the horizon.   The right side shows how the situation is improved by using a large rangefinder, which serves to decrease the angle θ.

Figure 1

 You see it all boils down to the angle θ.   When d is extremely short in comparison to the measured distance r, the angle θ creeps ever closer to becoming 90°, a situation which severely impacts the rangefinder’s accuracy due to the impact on the tangent of θ.  

Let’s see what the situation looks like numerically.   The smaller rangefinder has a length, d, equal to 3 feet.   Using it we measure θ to be 89.97°.   Plugging these numbers into the rangefinder distance measuring formula, we measure the distance to the ship to be:

r = d × tan(θ)

r = 3 feet × tan(89.97°)

r = 5729 feet

 Now let’s take a second measurement with the bigger rangefinder on the right.   This one has a length d equal to 60 feet.   You might be asking yourself, Do they really come that big??   Yes, before radar technology came on the scene to take their place, it was possible to find rangefinders as big as 60 feet in length!   Using the larger rangefinder we find θ is equal to 89.34° and the distance to the ship is calculated to be:

r = d × tan(θ)

r = 60 feet × tan(89.34°)

r = 5208 feet