Further Limitations of an Optical Rangefinder

As We discussed earlier that when optical rangefinders are used to measure the distance to objects extremely far away we encounter problems.   We discussed one of them last time, the fact that as θ approaches 90° the tangent of θ becomes asymptotic, resulting in a situation where even the most minute changes to θ bring about huge corresponding changes to the distance, r, we seek to measure.

This difficulty goes hand in hand with another we’ll be discussing today, the problem of very tight spaces.   They both lead to a greater potential for measurement inaccuracies.

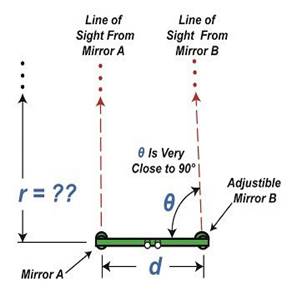
The rangefinder in Figure 1 depicts the kind of situation that often results when attempting to measure objects that are extremely far away, like a ship on a distant horizon.  Angle θ is very close to being 90°.   Let’s see what that does to our measuring attempts with the rangefinder’s on-board measuring scale, its indicator gauge.

Figure 1

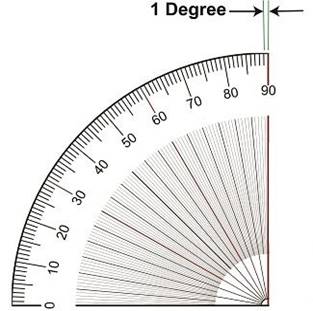
The fact is, when a [rangefinder] indicator gauge hovers near 90°, it becomes user unfriendly.   To illustrate, let’s refer to a common everyday protractor, shown in Figure 2.

Figure 2

Protractors are divided into 1° gradations, which allow us to measure angles between 0° and 90°.   This interval is fine for many angle measuring purposes, but we’ll see in a moment why it doesn’t work when measuring extremely long distances.

A similar protractor is found on a rangefinder’s indicator gauge, enabling us to measure the angle θ.   Notice how small the space is between 89 and 90 degrees.   Now imagine having to split that area into hundreds, even thousands, more gradations in order to accurately assess the value of θ.   This is precisely the situation we encounter when using a rangefinder to measure extremely long distances where the lines of sight form long, narrow triangles and θ hovers near 90°.   Are you beginning to see — or rather not see — the problem?

When this situation exists, ultra fine gradations must be made between the 89th and 90th degrees in order to make an accurate measurement of θ .  This results in a situation where gradation marks are spaced so closely together they become difficult, if not impossible, for the unaided human eye to read.