The Mathematical Link Between Gears in a Gear Train

 Previously we analyzed the angular relationship between the Force and Distance vectors in this simple gear train.   here we’ll discuss about  commonality between the two gears in this train which will later enable us to develop individual torque calculations for them.

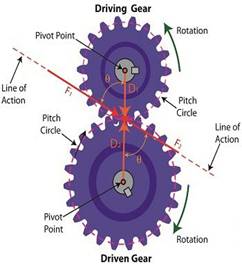
From the illustration it’s clear that the driving gear is mechanically linked to the driven gear by their teeth.   Because they’re linked, force, and hence torque, is transmitted by way of the driving gear to the driven gear.   Knowing this we can develop a mathematical equation to link the driving gear Force vector F₁ to the driven gear Force vector F₂, then use that linking equation to develop a separate torque formula for each of the gears in the train.

We learned in the previous topic in this series that F₁ and F₂ travel in opposite directions to each other along the same line of action.   As such, both of these Force vectors are situated in the same way so that they are each at an angle value ϴ with respect to their Distance vectors D₁ and D_2.   This fact allows us to build an equation with like terms, and that in turn allows us to use trigonometry to link the two force vectors into a single equation:

F = [F₁ × sin(ϴ)] – [F₂ × sin(ϴ)]

where F is called a resultant Force vector, so named because it represents the force that results when the dead, or inert, weight that’s present in the resisting force F₂ cancels out some of the positive force of F₁.

  Next topic we’ll simplify our gear train illustration and delve into more math in order to develop separate torque computations for each gear in the train.