Mechanical Advantage of a Compound Pulley

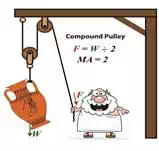
In this Topic series on pulleys we’ve gone from discussing the simple pulley to the improved simple pulley to an introduction to the complex world of compound pulleys, where we began with a static representation.   We’ve used the engineering tool of a free body diagram to help us understand things along the way, and today we’ll introduce another tool to prepare us for our later analysis of dynamic compound pulleys.   The tool we’re introducing today is the engineering concept of mechanical advantage, MA, as it applies to a compound pulley scenario.

The term mechanical advantage is used to describe the measure of force amplification achieved when humans use tools such as crowbars, pliers and the like to make the work of prying, lifting, pulling, bending, and cutting things easier.   Let’s see how it comes into play in our lifting scenario.

During our previous analysis of the simple pulley, we discovered that in order to keep the urn suspended, Mr. Toga had to employ personal effort, or force, equal to the entire weight of the urn.

F = W                                    (1)

By comparison, our earlier discussion on the static compound pulley revealed that our Grecian friend need only exert an amount of personal force equal to 1/2 the suspended urn’s weight to keep it in its mid-air position.   The use of a compound pulley had effectively improved his ability to suspend the urn by a factor of 2.   Mathematically, this relationship is demonstrated by,

F = W ÷ 2                              (2)

The factor of 2 in equation (2) represents the mechanical advantage Mr. Toga realizes by making use of a compound pulley.   It’s the ratio of the urn’s weight force, W, to the employed force, F.   This is represented mathematically as,

MA = W ÷ F                            (3)

Substituting equation (2) into equation (3) we arrive at the mechanical advantage he enjoys by making use of a compound pulley,

MA = W ÷ (W ÷ 2) = 2           (4)

Mechanical Advantage of  a Compound Pulley