Using a
Free Body Diagram to Understand Simple Pulleys
|
Sometimes
the simplest alteration in design results in a huge improvement, a truth I’ve
discovered more than a few times during my years as an engineering
expert. Last time we introduced the simple pulley and revealed that its usefulness was limited to the
strength of the pulling force behind it. Hundreds of years
ago that force was most often supplied by a man and his
biceps. But ancient Greeks found an ingenious and simple way
around this limitation, which we’ll highlight today by way of a modern design
engineer’s tool, the free body diagram. Around
400 BC, the Greeks noticed that if they detached the simple pulley from the
beam it was affixed to in our last blog and
instead allowed it to be suspended in space with one of its rope ends fastened
to a beam, the other rope end to a pulling force, something interesting
happened.
The Simple Pulley Improved It
was much easier to lift objects while suspended in air. As a
matter of fact, it took 50% less effort. To understand why,
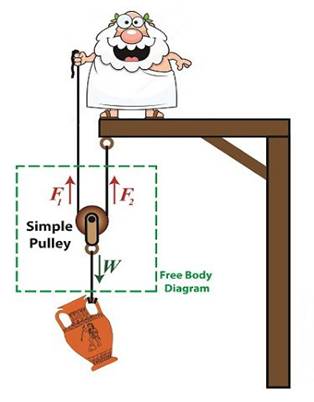
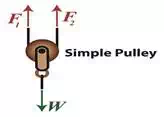
let’s examine what engineers call a free body diagram of the pulley in our
application, as shown in the blue inset box and in greater detail below.
Using a Free Body Diagram to Understand
Simple Pulleys The
blue insert box in the first illustration highlights the subject at
hand. A free body diagram helps engineers analyze forces acting upon a stationary object
suspended in space. The forces acting upon the object, in
our case a simple pulley, represent both positive and negative
values. The free body diagram above indicates that forces
pointing up are, by engineering convention, considered to be positive, while
downward forces are negative. The basic rule of all free
body diagrams is that in order for an object to remain suspended in a fixed
position in space, the sum of all forces acting upon it must equal zero. We’ll
see how the free body diagram concept is instrumental in understanding the
improvement upon the action of a simple pulley next time, when we attack the
math behind it. |