Gear Reduction Worked Backwards

 Previously we saw how a gear reduction does as its name implies, reduces the speed of the driven gear with respect to the driving gear within a gear train.   Today we’ll see how to work the problem in reverse, so to speak, by determining how many teeth a driven gear must have within a given gear train to operate at a particular desired revolutions per minute (RPM).

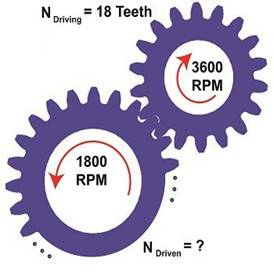
 For our example we’ll use a gear train whose driving gear has 18 teeth.  It’s mounted on an alternating current (AC) motor turning at 3600 (RPM).   The equipment it’s attached to requires a speed of 1800 RPM to operate correctly.   What number of teeth must the driven gear have in order to pull this off?   If you’ve identified this to be a word problem, you’re correct.

 Let’s first review the gear ratio formulas introduced in my previous two articles:

R = n_Driving ÷ n_Driven             (1)

R = N_Driven ÷ N_Driving             (2)

Our word problem provides us with enough information so that we’re able to use Formula (1) to calculate the gear ratio required:

R = n_Driving ÷ n_Driven = 3600 RPM ÷ 1800 RPM = 2

This equation tells us that to reduce the speed of the 3600 RPM motor to the required 1800 RPM, we need a gear train with a gear ratio of 2:1.   Stated another way, for every two revolutions of the driving gear, we must have one revolution of the driven gear.

Now that we know the required gear ratio, R, we can use Formula (2) to determine how many teeth the driven gear must have to turn at the required 1800 RPM:

R = 2 = N_Driven ÷ N_Driving

2 = N_Driven ÷ 18 Teeth

N_Driven = 2 × 18 Teeth = 36 Teeth

The driven gear requires 36 teeth to allow the gear train to operate equipment properly, that is to say, enable the gear train it’s attached to provide a speed reduction of 1800 RPM, down from the 3600 RPM that is being put out from the driving gear.

But gear ratio isn’t just about changing speeds of the driven gear relative to the driving gear.