Relationship between Modulus of Elasticity and Modulus of Rigidity

Modulus of elasticity () and the modulus of rigidity () are related by the following equation:

$E=2G\left( 1+\nu\right)$

Here, $\nu$ represents a number called Poisson’s ratio given to the particular material. When the material is being stretched in one direction, it gets shortened in a perpendicular direction. In the direction that the material becomes elongated, the axial strain ( $\varepsilon_a$ ) is defined as the fractional increase in the length. In the direction that the material shortens, the transverse strain ( $\varepsilon_t$ ) gives the fractional reduction in length. The diagram below illustrates these changes in shape:

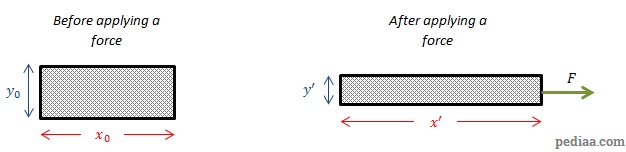
Difference Between Modulus of Elasticity and Modulus of Rigidity - Poisson's_Ratio_Illustration

Defining Poisson’s ratio

In this diagram, the axial strain is:

$\varepsilon_a=\frac{x'-x_0}{x_0}$

The transverse strain is:

$\varepsilon_t=\frac{y'-y_0}{y_0}$

Note that since the object shortens in the direction perpendicular to the force, $\varepsilon_t<0$ . Poisson’s ratio ( $\nu$ ) is defined as:

$\nu=-\frac{\varepsilon_t}{\varepsilon_a}$

The minus sign has been introduced to ensure that $\nu$ takes a positive value.