Basic Worm Gear Design Calculations Using AGMA Empirical Formula

Worm gears are widely used in industrial settings and in automobile gear boxes. This worm gear design tutorial will discuss the basics of the worm gear box design calculation using the AGMA empirical formula.

A worm gear box must contain a worm and a mating gear (helical gear) and normally the axis of the worm is perpendicular to the axis of the gear. Look at the picture below:

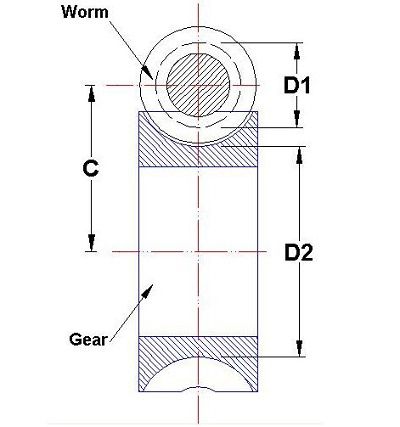
Where,

D1 – Pitch Diameter of Worm

D2 – Pitch Diameter of Gear

C – Centre to Centre Distance between the Worm and the Gear

This worm gear design tutorial will discuss up to the selection of the module and pitch and the calculation of the number of teeth, pitch circle diameter and centre to centre distance between the worm and gear. We will use the AGMA formulae for doing the calculations. Design calculations of the other aspects of the worm gear will be discussed in a subsequent part of the tutorial.

Steps of the Design Calculation

○ The axial pitch of the worm and the circular pitch of the gear must be same for a mating worm and gear. We will use the term Pitch (P) for both the pitch in this tutorial.

○ Also, the module of the worm as well as the gear must be equal for a mating worm and gear.

○ Now, let’s say we have the following design input:

Speed of the Worm (N1) = 20 RPM

Speed of the Gear (N2) = 4 RPM

○ And, we have to find out the Module (m), Pitch (P), Number of helix of Worm (T1), Number of teeth of Gear (T2), Pitch circle diameter of Worm (D1), Pitch circle diameter of Gear (D2), Centre to centre distance(C).

○ Select the suitable module and its corresponding pitch from the following AGMA specified table:

Module m (in MM) - Pitch P (in MM)

2 -------------------------6.238

2.5 ---------------------- 7.854

3.15 --------------------- 9.896

4 ------------------------- 12.566

5 ------------------------- 15.708

6.3 ----------------------- 19.792

8 -------------------------- 25.133

10 ------------------------- 31.416

12.5 ----------------------- 39.27

16 -------------------------- 50.625

20 -------------------------- 62.832

○ Say, we are going ahead with the Module as 2 and the Pitch as 6.238.

○ Use the following gear design equation:

N1/N2 = T2/T1

And, we will get:

T2 = 5 * T1……………….Eqn.1

○ Now use the following AGMA empirical formula:

T1 + T2 > 40………………Eqn.2

○ By using the two equations (Eqn.1 & Eqn.2), we will get the approximate values of

T1 = 7 and T2 = 35

○ Calculate the pitch circle diameter of the worm (D1) by using the below AGMA empirical formula:

D1 = 2.4 P + 1.1 = 16.0712 mm

○ The following AGMA empirical formula to be used for calculating the pitch circle diameter of the gear (D2):

D2 = T2*P/3.14 = 69.53185 mm

○ Now, we can calculate the centre to centre distance (C) by the following equation:

C = (D1 + D2)/2 = 42.80152 mm

○ The below empirical formula is the cross check for the correctness of the whole design calculation:

(C^0.875)/2 <= D1 <= (C^0.875)/1.07

Observe that our D1 value is falling in the range.

Conclusion

The worm gear box design calculation explained here uses the AGMA empirical formulas.