Difference between Tensors and Vectors

What are the differences between the vector and the tensor? What are the relation between the mechanical rotations vectors and tensors? This topic will also cover these all.

Vector

Any quantity that has both magnitude and direction is called a vector. Velocity, acceleration, and force are a few examples of mechanical vectors.

So, from the definition above it should be clear that every vector must have two components: the magnitude component and the direction component.

Representations of vector

In three dimensional space, a vector is represented by its X, Y, Z components. The magnitude part of the vector is expressed by the matrix of numbers, and the direction part of the vector is expressed by the matrix of unit vectors.

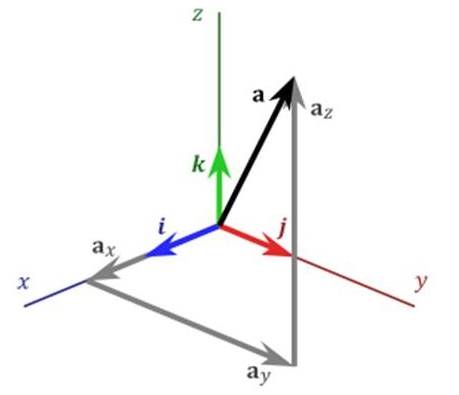
In the adjacent picture, the vector a, which has three scalar components ax, ay, and az and three unit vectors i, j, k along X, Y and Z, can be represented as:

a= ax i + ay j + az k……………………(1.1)

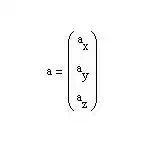
In the matrix representation of the vector, the starting point of the vector is implicitly considered to be at the origin of the representing co-ordinate system and this is how the vector is different than a point.

The above vector can also be represented in matrix form as:

Multiplication of vector with another vector

The following MathCAD example is showing the inner product of two vectors:

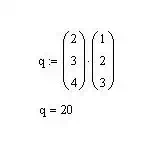
And the result is 20, which is a scalar quantity. So, it can be concluded that the inner product of the two vectors produce a scalar quantity.

Multiplication of vector with a scalar

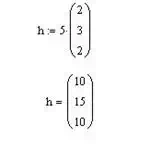
So, by multiplying by a scalar quantity, all the three components of the vector have scaled up proportionately or, in other words, the vector changed its magnitude without changing its direction.

Tensors

By, now you know that if you want to change only the magnitude of a vector without changing its direction, you will go for the multiplication of the vector with a scalar quantity.

In case you want to create a new vector with a different magnitude as well as direction (than the initial vector) then you have to multiply the initial vector with another type of mathematical entity called a tensor.

The tensor is a more generalized form of scalar and vector. Or, the scalar, vector are the special cases of tensor.

○ If a tensor has only magnitude and no direction (i.e., rank 0 tensor), then it is called scalar.

○ If a tensor has magnitude and one direction (i.e., rank 1 tensor), then it is called vector.

○ If a tensor has magnitude and two directions (i.e., rank 2 tensor), then it is called dyad.

○ And so on...

Please note that there are differences between the term “direction" and the term “dimension." All the types of tensor (scalar, vector, and dyad) can be defined in a three dimensional space or co-ordinate system.

For describing a rank-1 tensor, one subscript should be sufficient. Refer the Fig.1 and the matrix representation of the vector a above for better clarity. You can think of a force vector for practical example.

For describing a rank-2 tensor or dyad, I will use the example of mechanical stress tensor below:

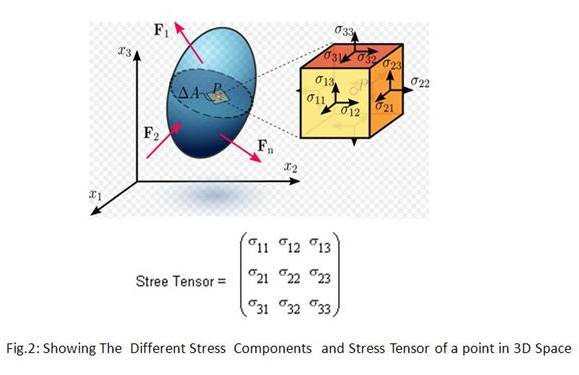
Please observe that each of the stress components of the stress tensor matrix has two subscripts, the first subscript is for the direction of area normal (the surface normal of the x2–x3 surface is 1 and so on) and the second subscript is for direction of the stress component.

So, the stress tensor (a dyad or rank-2 tensor) has two directions namely direction of area normal and the direction of stress component.

Mechanical Vector Rotations

Say, you have a vector and you want to change the direction of it then you have to go for the vector rotation.

For rotating the vector, multiply the vector with the rotation matrix and you will get the rotated vector.

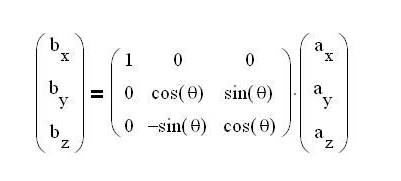
In the above example the vector a is rotated by angle θ about X axis and the vector b is produced.

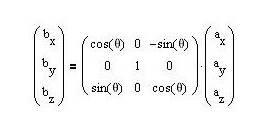
In the above example the vector a is rotated by angle θ about Y axis and the vector b is produced.

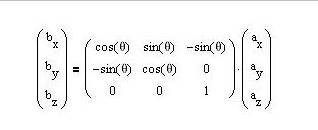
In the above example the vector a is rotated by angle θ about Z axis and the vector b is produced.

Please note that the rotation matrix is also a 3X3 matrix but it is not necessarily a tensor. Tensor is a physical object and in a tensor matrix there are certain relations between the different elements of it.

Conclusion

Tensor is the generalized form of vectors and scalars. All matrixes cannot be a tensor unitary; to be a tensor the matrix elements must follow certain relations among each other. A vector can be rotated by multiplying it by a rotation matrix.