Calculation Methods for Pulley Systems

The article explains the three fundamental systems of pulleys, covering their operational description and methods for calculating their velocity ratio, mechanical advantage, and efficiency.

From ancient times man has always been keen in devising machines of different kinds for one basic reason: relieving humans from tasks that are tedious and involve massive efforts. Pulley mechanisms are one of these machines that have been serving mankind since the day they were invented.

A pulley mechanism consists of a wheel and string assembly and is designed for lifting heavier loads through a comparatively lower magnitude of effort. The mechanism can be better understood by studying the behavior of a “simple pulley."

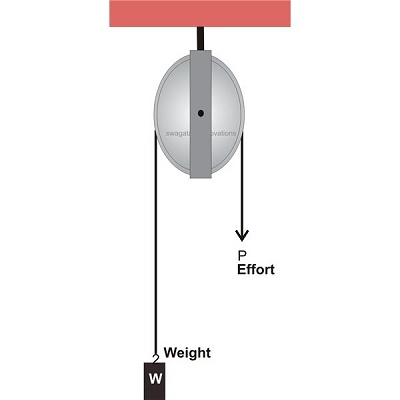
Simple Pulley: A simple pulley basically consists of two components, the wheel and the string; the wheel may be made up of wood or metal and includes a grove cut along its circumferential periphery. The string is allowed to slide or pass through this groove with a load that is to be lifted fixed at one of its ends and an effort applied at the other end in order to lift the load. The pulley wheel is supported over a rigid frame about its central axis.

 The applied effort through pulling of the string rotates the pulley and pulls the load upwards, helping the load to be lifted with ease.

A classic example of this mechanism can be witnessed over wells where the pulley and rope are used for lifting water-filled buckets.

Some important observations made by assessing this mechanism which may prove useful while calculating them are described below:

○ The weight of the pulley block can be ignored as its too small compared to the load that’s required to be lifted or rather moving heavier weights become more desirable for efficient response from these devices.

○ The friction developed on either side of the pulley across the string contact can also be ignored, again due to its negligible occurrence.

○ Calculations prove that the Mechanical Advantage (MA) and Velocity Ratio (VR) of this mechanism is unity under the discussed operational conditions.

In order to improve MA, VR, and efficiency, the above pulley mechanism is dimensioned through some intelligent combinations of extra pulleys and strings. These specialized pulley mechanisms are classified as follows, so let’s study them one by one.

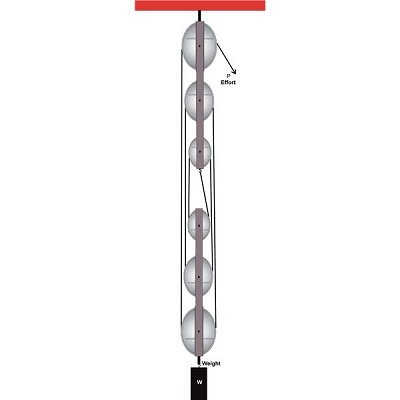
First System of Pulleys

As can be seen from the diagram, the lowermost pulley here carries the load (being lifted), which is fixed and hangs over the axle of the pulley.

An end of the string T1 attached firmly to an upper rigid frame, passes across the groove of this pulley and attaches its other to the axle of the second.

The same string configuration is repeated for the all the pulleys until the first pulley where the preceding pulley’s string end instead of attaching to the axle of the topmost pulley, slides down across its groove and ends towards the other side where the effort can be finally applied.

The applied effort lifts the weight and also the entire pulley system under the topmost pulley.

Now, suppose if the applied effort raises the weight W and the pulley P1 by x meters, in order to maintain tightness of the string attached to its axle and balance the movement, pulley P2 has to move through a distance of 2x meters.

The same theory applies to the pulley P3 which now must show a relative displacement of 2 × (2x) = 22x, also the pulley P4 must compensate the act with an upward lift of 2 × 22x = 23x and finally for the pulley P4 which is fixed with the upper frame, the string takes over the sequence to produce a displacement equal to 2 × 23x = 24x.

Therefore Velocity Ratio = Distance covered by effort/Distance covered by load

= 24x/x = 24

Therefore if the above pulley system carries n number of pulleys then VR = 2n

And MA = W/P (standard equation)

Also efficiency ɳ = MA/VR

Second System of Pulleys

The diagram below shows the second system of pulleys consisting of two blocks. The upper block carries three wheels which freely rotate about their individual central axes and are supported over a single common axle which is firmly fixed to a rigid upper frame.

The lower block also contains similar pulley and axle mechanism; however the whole structure is supported by one end of an intertwined string configuration passing through the pulleys, as illustrated in the figure. The other end termination of the string which passes across the uppermost pulley is used for the application of the effort. The weight is supported by the axle of the lower block.

Through some observation it becomes obvious that for displacing the weight by some distance, say x, the applied effort has to move through a distance nx, where n is the total number of pulleys in the system.

Therefore, the velocity ratio can be expressed as nx/x = n

And as usual MA and the efficiency may be written as given for the first system of pulleys.

Third System of Pulleys

It is quite identical to the first system; however by looking at the figure it becomes clear that the operations involved are just in the reverse process.

The velocity ratio of the system can be tracked by following a unit movement of the weight.

Suppose, the attached weight is moved by a distance of x meters by the effort applied at P, this will cause an instantaneous slackening of the strings involved.

For supporting the action, the strings will go through a sequential tightening movement through the pulley rotations.

Therefore the slackening of string 1 (assuming to be equal to x meters) is compensated by pulley number two, which comes down and covers a distance of 2x meters.

Also with slackening of string 2, x1 gets pulled across a distance of 2x –x = x meters.

Continuing further, with x1 being pulled through x meters, x2 gets pulled through a length of 2x +x = 3x = (22 – 1)x.

The procedure is followed on to keep the relative position of pulley 3 constant and string 3 is pulled across a distance of (2 × 3x × x) = 7x = (23 – 1)x, and finally string x4, which is actually the effort, crosses a distance of (2 × 7x + x) = 15x = (24– 1)x meters.

Therefore the VR of the system can be equated as = Distance Covered by Effort/Distance Covered by Weight = (24 – 1)x/x = 24 – 1, for the present example which consists of 4 pulleys.

In general for a particular third system of pulley having n number of pulleys, VR = 2n – 1.

MA and ɳ may be taken as discussed for the previous systems.