Working with Data Tables - Basic Skills for Engineers and Machinists

Arranging information into orderly rows and columns is one of the most common forms of communicating precision tabular data.

A multiplication or times table is probably the very first data table any student learns. Many people memorize it and keep it in mind their entire life. Some folks use it as a tool, refering to it several times a day for tasks like calculating payments, and computing gas consumption and remaining distance, etc.

Engineers, as well, need to use different data tables to do their routine duties. Tables used in a day's work may range from trigonometric, logarithm, and statistics tables to thermodynamics and material specification tables. Over time, as far as it was possible to accurately compute the data involved, tools like slide rules, nomographs, scientific and engineering calculators, and, these days, computers have evolutionally benefited engineering. Despite technological advances, much engineering data is still presented, and used, in the form of rows and columns. Examples of these are specifications of structural profiles like I-beams, C-beams, L-beams, pipes and tubes, metallurgical specification of metallic alloys, characteristics of semiconductors, etc. Working with data tables is the ability that enables engineers to do their job in a professionally granted manner.

What is a Data Table?

Data tables are a means of arranging data into an information format. Since data are often viewed as the lowest level of abstraction from which information and then knowledge are derived (ref. Wikipedia, Data), it is usually a collection of numbers, words, figures, etc. that result from data collection activities. When data is processed and arranged in such a way that satisfies certain queries, it is known as information. The basic Idea of arranging data into information format is the field and record concept. A record consisting of several fields gives information about a specific Item. Fields are attributes of the subject item of the record. Data tables are collection of records arranged as rows of the table while columns of the table represent the fields of these records.

Example of an Engineering Data Table

Imagine that an engineer is designing a steel structure and as a result of his analysis is looking for a suitable beam profile to withstand a certain applied force.

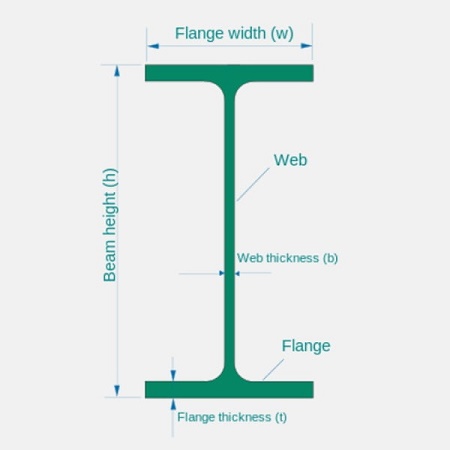
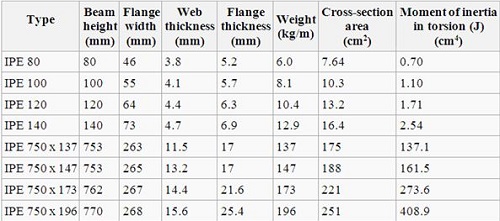
Looking up cross-section areas of candidate I-beam profiles in a data table such as shown below for European standard beams, IPE, he can calculate sheer stresses for different profiles and choose the one that satisfies design criteria such as material specification, minimum weight, and suitable dimensions.

Of course the above example is the primitive, and perhaps the old way, of designing structures and nowadays there is sophisticated engineering software that embeds necessary data tables and facilitates these engineering tasks.

Table: From Wikipedia, I-beam

Other Engineering Applications

Using data tables to look for or represent required information is not the only engineering application of data tables. They may have other engineering applications such as different numerical analysis approaches, for instance, to solve tedious high order nonlinear equations, simulate engineering systems by modeling these systems in the form of differential equations and solving these equations. In practice organized data may be applied in any numerical analysis approach.

Data tables may also be applied in quality assurance approaches to represent, for instance, FMEA (Failure Mode and Effect Analysis) charts, Control Plans, or statistical data.

It is obviously clear that applications for data tables in engineering are not limited to the above examples and description of any of these applications in particular may take an independent article. However, we include some real-world usage examples below.

How to Make a Data Table

The simplest way to create a data table is drawing the table with adequate rows and columns on paper by pencil and ruler, and filling the created cells with appropriate gathered, measured, and/or calculated data. A more effective way is doing the same thing in a computerized spreadsheet. Whatever approach taken, each row should contain different attributes of an entity which is usually the subject of the data table.

Key attributes like Name, ID, and/or independent variables are usually on the left side of the table. Then there are gathered and/or measured data and other dependent variables, and finally calculated, concluded, and/or summarized data and comments on the right side. This way Items of each column should be of the same nature and unit, for instance in the above example beam height is in mm, weight of unit length is in Kg/m, and cross-section area is in cm2.

Usage Example 1: Using a Data Table to Summarize and Order Materials in a Project

Years ago while as a production manager I was assigned to manufacture parts, fabricate subassemblies, and assemble stone crusher plants. I used spreadsheet software on a 80286 MS-DOS PC to summarize and order materials to be used in the project.

Materials were mostly in the form of structural profiles like I-beams, C-beams, L-beams, and plates, as well as fasteners along with machinery and equipment. We had a part list sorted by subassemblies, machinery, and equipment. There was not much problem with machinery and equipment.

The main problem was with materials to be used in subassemblies because individual lengths of structural elements of each subassembly were given in the parts list. Types of materials for different subassemblies were more or less similar, for instance, different lengths of a type of I-beam was supposed to be used in several subassemblies, and that I-beam was available in 12 meters length in the market. So we had to order the 12 meters beams and later cut them to desired lengths.

In the spreadsheet software a data table was created for these types of materials and the attributes of each structural element was entered in the table, which was later sorted by the type of material. In this way, different individual lengths of each type of material could easily be combined together and later divided by the available lengths in the market.

As a result of this attempt, raw materials were reduced to about thirty types, and the required quantity of each type was ordered and purchased.

Usage Example 2: How a Data Table Was Used to Solve an Equation

Once I was involved in designing a threaded rod which was supposed to be made by the thread rolling process, as shown below. Thread rolling is a process that forms the threads by material flow, pushing some material from beneath the blank diameter to above the blank diameter. Thus the blank diameter should be between minimum and maximum diameters of the thread. Technical documents from the thread rolling tool manufacturer suggested that this diameter should be very close to the pitch diameter of thread. However, in practice we found out that the blank diameter should precisely be determined because larger blank diameters would lead to larger major diameter and tighter fit within the nut, and smaller blank diameter would lead to smaller major diameter and looser fit within the nut. To keep thread diameters within functional tolerances, we had to determine blank diameter with hundredth of millimeter precision.

The concept to calculate blank diameter was volume of material pushed above the blank diameter is equal to the volume of material moved from beneath the blank diameter. This way an equation could be derived in which blank diameter was the only unknown. At the first sight this solution seemed very simple, but in practice we had an equation of the fourth order with long complicated terms which was written in more than two pages. Solving this equation was a tedious job with too much uncertainty due to probable mistakes during calculation.

We had to find another solution and this solution was obviously to use a data table. Using a spreadsheet application we created a data table in which the first column of the left side was assigned to the bank diameter, and the middle columns were assigned to necessary thread profile elements required to calculate volumes of peak and valley of the thread profile. Last column at the right side was assigned to the difference between peak volume and valley volume of the thread profile with a four-digit decimal point.

After filling the blank diameter column with numbers ranging from a value adequately less than pitch diameter to a value adequately more than pitch diameter with one hundredth of millimeter step spreadsheet calculated the results and we had the answer. The answer was verified in action and with a very slight modification in hundredth of millimeter the blank diameter was determined.