Calculate Mass Moment of Inertia for Irregular Geometry in Six Steps

This article will explain how to calculate the mass moment of inertia of an irregular geometry. You need not use any tools for calculating the mass moment of inertia. Just learn the basics and calculate the mass moment of inertia manually in six simple steps.

The mass moment of inertia is frequently used for mechanical design calculations of rotational bodies. Most of the time you will deal with regular geometries (like cylinders, spheres, etc.) for which mass moment of inertia values can be calculated using standard tables. For the irregular geometries, standard formulas are not available and you have to actually start from the basics. The example below will give you an idea of how to proceed for moment of inertia calculations of any irregular shapes.

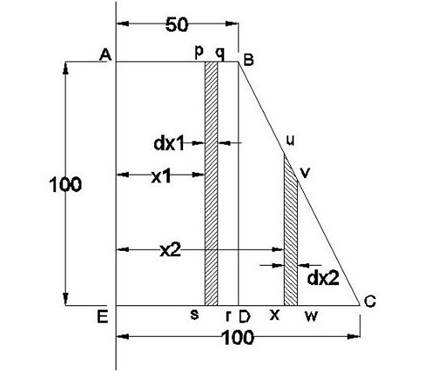
Say, you need to calculate the mass moment of inertia about the side AE of the plate ABCDE . You will see this type of plate in a flat plate heat exchanger. The thickness of the plate is 5 and density is 1. You have to proceed as below:

Step-1

Divide the whole area to some similar kinds of area. In our case we have divided the area (ABCDE) to one rectangle (ABDE) and a triangle (BCD).

Step-2

Next, you have to use the mass moment of inertia equation:

I = ∫r2 dm………..eqn.1.1

Where,

dm – The mass of a very small slice, which is parallel to the axis about which the mass moment of inertia to be calculated

r – The distance of dm from the axis

Step-3

But, since we have divided the whole area to two different areas, so, the eqn1.1 will be modified as:

I = 050∫x12 dm1 + 50100 ∫x22 dm2 ………..eqn.1.2

Where,

dm1 – The mass of the small slice pqrs

x1 – The distance of the slice pqrs from the axis AE.

dm2 – The mass of the small slice uvwx

x2 – The distance of the slice uvwx from the axis AE.

Step-4

Now, write “dm1" in terms of “dx1". And it will become:

dm1 = volume * density

= 100 * 5 * dx1 * 1

Step-5

Similarly write “dm2" in terms of “dx2" like below:

dm2 = {200 – (100/50)*x2} * 5 * dx2 *1

Step-6

Now by putting the values of the dm1 and dm2 in eqn1.2 we can get the value of the mass moment of inertia of the plate about the axis AE as:

I = 500*[(x1)3 / 3] 0 50 + 500*[(x23 / 3) - (x24 / 4)] 50100

= 78125000

Conclusion

In practical mechanical design calculations you may have to calculate mass moment of inertia for the irregular geometry. In that case you can either follow the basic calculation procedure as shown in this article or you can use CAD packages like ProE or AutoCAD. Or you can use both in order to ensure the accuracy of your calculation.