Before entering to the main topic of stress-strain curve we have to know about stress and strain. elasticity and plasticity, hook’s law and young’s modulus of elasticity.
What is stress ?
If a applied force causes change in the dimension of the material then the material is in the state of stress. If we divide the applied force, F by the cross sectional area , A then we will get the stress.
The symbol of stress is σ (Greek letter sigma). For tensile and compressive forces. The unit of stress is the pascal, Pa, where 1 Pa = 1 N/m. For ease of use most of the time Mega pascal, MPa is used as a units of stress.
σ = F/A
For tensile and compressive forces area taken is right angles to the applied force. For shear force area is taken parallel to the applied force. And the symbol used is tau, τ for depicting the shear stress.
What is strain ?
Change in the dimension with respect to the original dimension due to stress is known as strain. It is denoted by the symbol epsilon.
ε = x/ L
For a shear force, strain is expressed by γ (gamma)
Elasticity
It is the property of the material which enables the material to retain its original form after the external force is removed.
Plasticity
It is property which makes the material permanently deformed without breaking even after the force is removed .
These definitions are important for understanding the Stress Strain relationship .
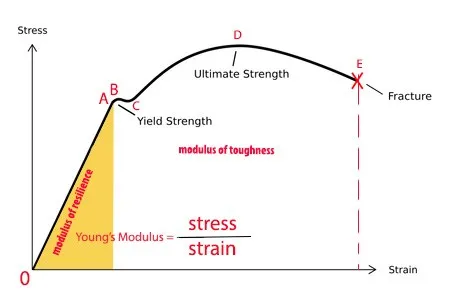
If tensile force is applied to a steel bar it will have some extension. If the force is small the ratio of the stress and strain will remain proportional. And the graph will be a straight line ( up to point A) . So the 0 to point A is the limit of proportionality.
If the force is considerably large the material will experience elastic deformation but the ratio of stress and strain will not be proportional. (point A to B). This is the elastic limit. Beyond that point the material will experience plastic deformation. The point where plastic deformations starts is the yield point which is show in the figure as point B. 0 B is the upper yield point. Resulting graph will not be straight line anymore. C is the lower yield point. D is the maximum ultimate stress. E is the breaking stress.
Hooke’s law: Within the proportional limit strain is proportionate to stress.
Young’s modulus of elasticity
Within the proportional limit, stress α strain, hence stress = E × strain
E is a proportionality constant known as Modulus of elasticity or Young’s modulus of elasticity.
This constant of proportionality is called Young’s modulus of elasticity and is given the symbol E.
E has the same unit as the unit of stress because strain is dimensionless.
E = σ / ε Pa
Another two terms are important in the stress strain graph of mild steel these are
Modulus of Resilience: It is the area under the curve which is marked by the yellow area. It is the energy absorbed at unit volume up to elastic limit.
modulus of resilience = 1/2 x σ x ε = 0.5 x (FL/AE)
Modulus of toughness: It is the area of the whole curve (point 0-E). Energy absorbed at unit volume up to breaking point.