Modal Submodeling

Submodeling is an important technique in finite element analyses that allows us to get a more accurate answer in a local region of a larger model.  Often computational and time limitations prevent us from using as fine a mesh as is required to adequately assess the results in all local regions of a large complex model.

A submodel is an independent, more finely meshed model of a region of interest within the global model. Submodeling uses a cut-boundary displacement method; displacements calculated by the full model are specified as boundary conditions for the submodel.  Submodeling is based on St. Venant's principle, which states: the difference in effects due to two statically equivalent loadings becomes insignificant as the distance from the load application increases. Therefore, if the boundaries of the submodel are far enough away from the area of interest, accurate results can be calculated in the submodel.

The process of performing a submodel analysis is well documented for static analyses, but, what if we wanted to do a submodel of a modal analysis?  We are out of luck, right?  Any non-zero displacements applied in a modal analysis are treated as 0.  So how can we apply cut boundary displacements to a modal analysis?

Well, it turns out that there is a technique for doing a submodel of a modal analysis! The trick is that we use a forced harmonic analysis to do it.  First, run a modal analysis on the global model with a mesh reasonable enough to capture accurate mode shapes, but perhaps not sufficient enough to resolve accurate stresses.  For the mode of interest we use submodeling tools to extract displacements at the cut boundaries of the submodel.  Then, we perform a harmonic analysis at the exact frequency calculated in the modal analysis.

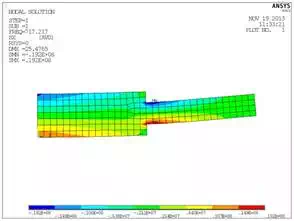
For example, let’s look at a modal analysis of a stepped cantilevered beam.  We run the modal analysis with a fairly coarse mesh and exclude the fillets at the step.

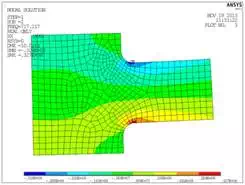
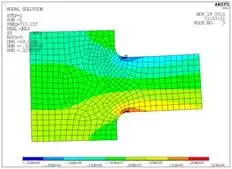
From the modal analysis results, we extract the displacement for the first mode at 2 cut locations and apply these displacements in a harmonic analysis of a submodel with a finer mesh and the fillets included.  The harmonic analysis is run at a single frequency, matching the frequency of the mode of interest (717.2 hz in this case).

This allows us to get a more accurate stress distribution in the region.  While the magnitude of modal stresses is normalized, obtaining an accurate stress distribution is still important.

This technique can be extended to pre-stressed modal analyses.  You would need to use standard static analysis submodel techniques to generate a pre-stress of the submodel, and then run a pre-stress harmonic analysis using the displacements from the model of interest.