A General Discussion on Ship Stability

Strength and Stability of a ship or any other marine structure are of major concerns for a Naval Architect. Ships, which are designed to give lifelong operations should have strength and efficiency as well as smooth performance. 

Stability is defined as the general tendency of a vessel or any other floating body to remain upright. A ship is said to be ideally stable if the line of action of the buoyancy coincides with the vertical centreline, i.e; the centre of buoyancy and the centre of gravity of the ship lies in the same line. 

Figure 1: A heeled ship

However, invariably in all seas, the ships have to face the same problems of waves, environmental vagaries and sometimes interplay of both in worse case scenarios. Moreover, internal factors like improper distribution of loads, structural breach or sometimes problems in maneuvering and course-keeping can drastically alter the stability of the ship; i.e its tendency to remain upright! 

Stability of a ship has to be calculated for every situation a ship have to face, whether it is sailing in normal conditions or facing with storms or even on the jetty/port.  Calculations and tests are carried out both during design phase and after construction for estimating and improving the ship efficiency.

INTACT STABILITY

A ship when not damaged is said to possess intact stability. Stability deals essentially with the rotational motion of the ship viz., Roll(heel) and pitch(trim), former being the rotation around the X axis (ship's longitudinal axis) and latter for Y axis (ship's vertical axis).       

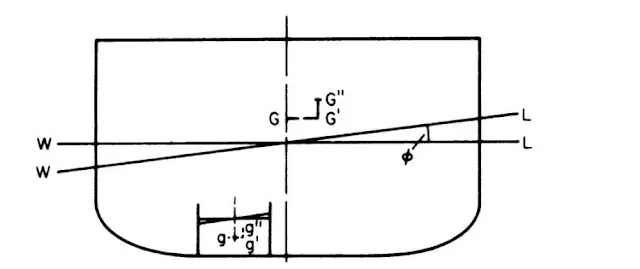
Take a Barge for illustration, Taking its Transverse section ( a plane along Y-Z axis ). Angle BMB’ = θ

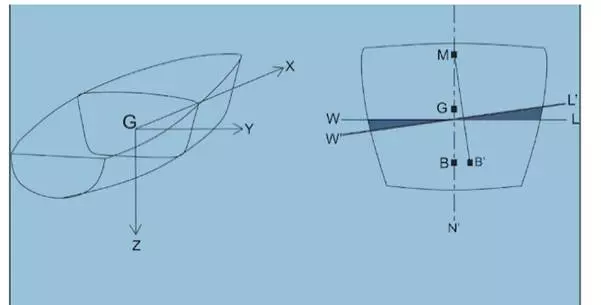
Figure 3

Let us assume it to heel by a small angle. Consequently, it's centre of buoyancy would change. However, it's centroid would remain same (assume no hanging weights and free liquids anywhere inside the ship). The line on which buoyant force acts is called line of action. Also the area of immersed and emerged wedges are equal. Now, as seen in the figure, Buoyant force and weight of the ship are making a couple acting in the opposite direction to the rolling motion. This will tend to undo the heel.

The points shown in the figure are very important. Point M (Metacentre point where the line of action meets the centreline of the ship), is most important, many of the calculations which are done deals with M.
The moment relation used for the righting arm (GZ) in the condition of heel is as follows:

                                                     GZ = sin θ*GM

where GM is the metacentric height measured from the Centre of Gravity and the Metacentre. 

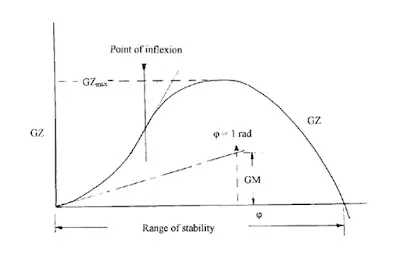
GZ Curves and Calculations 

These curves are drawn With GZ on the Y axis and Heeling angle on X axis. If we see the general GZ curve, for small angles, righting lever GZ is proportional to heeling angle and thus a tangent can be drawn through origin which gives GM.
Till the maximum GZ value, there is a variation in the rate of growth of GZ value, the point where rate tends to decrease is point of contraflexure and the angle is angle of contraflexure. Now, above points are valid only when neglect many factors which contribute to ship instability.

Figure 4: GZ Righting Curve of Stability

Area under the graph gives the energy stored.

This graph is of equal importance for both  naval architects and ship officers, while former draws this during design phase and latter every time before a voyage keeping in mind the path as well as the conditions they have to face (stability booklet is an important aspect in every voyage of a ship). 

In Submarines, the point M and B are coincident. Also for the stability G should be below B as opposite to any floatable.

FREE SURFACE EFFECT

This is a crucial problem pertaining to any stability factor of a vessel. As the ship heels, a pseudo force acts to any liquid which is present inside and thus the liquid changes its position thus changing the position of G, and we know with changing in G, values like GM, GZ would change and thus contribute to instability.

Figure 5: Wall Sided Ship with liquid contained in a wall-sided tank

Due to change in position of G, GM of the ship would change according to the following

formula : GM (new)=GM (old) -K (I / Displacement)

Where K is relative Density of liquid with respect to seawater

And I is moment of inertia of liquid surface on plane.

The factor has to be subtracted from the graph and a corrected set of GZ curve is obtained.

Special measures are taken to reduce free surface effect such as Bulkhead Division, filling the tank to brim etc.

If the heeling angle increases, and GZ lever in not enough to counterbalance the

heeling force, ballasting water in opposite side can be done, though draft would increase, but it would undo the heal at the same time. 

The factor has to be subtracted from the graph and a corrected set of GZ curve is obtained.

Hanging weights can have same effects be changing centre of gravity of the ships.

When the ship is unloading cargo with a crane on board, and it is on the verge to unload it on jetty, ship starts to heel and as soon as it keeps it on the jetty, it oscillates until it achieves upright condition.

Reduction in GM can also be seen during rotational motion when an aircraft or helicopter lands or takes off from a ship or an automobile moves in a RORO vessel.

Sometimes there is a permanent angle of heel or trim which may be due to uneven

distribution of weight or due to negative GM, former being called Angle of List and latter Angle of Loll. 

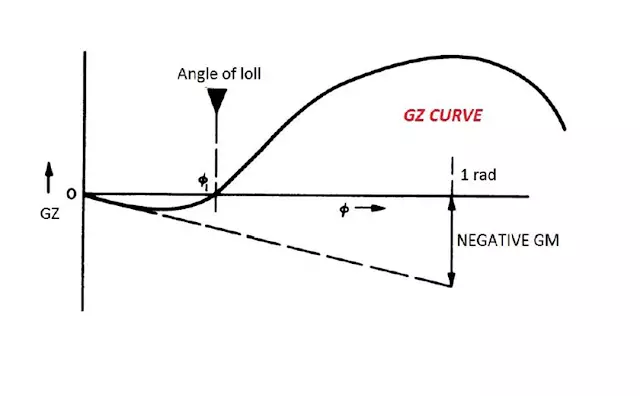
Angle of Loll

Due to negative GM at zero heel angle, the ship heels until it's GM becomes positive. This continual unbalanced heeling act takes place in an oscillatory fashion. 

Figure 6: GZ Curve indicating Angle of Loll

As shown in the figure, there is a negative GZ and consequently the tangent drawn also gives the negative GM. But as soon as the GZ starts to increase from 0, the tangent gives a positive GM.

 Now, if the ship heels further, same happens, but here the upright condition is not achieved, it would oppose the heel only till angle of loll. Angle of loll is due to external forces, it should not be confused with angle of list which is due to internal shift of moment forces.

Also at some considerable angle, the Deck starts to immerse, also knows as angle of deck immersion because it may be the maximum angle upto which rolling motion can be allowed because of open spaces at deck which may allow water to enter into the ship.

RORO vessel Cougar Ace ( IMO no. 9051375), which capsized in 2006 was reportedly being erroneously ballasted to undo its heel caused by a wave slap.  Though cause of the loss in stability is still not crystal clear,but speculations are that the ship had developed an angle of loll due to external force ( sea wave ) which would have caused the vehicles to displace and ultimately gaining an angle of list which heeled her further. Though she was

recovered and repaired. She is wall sided and have a large freeboard which then allowed her to prevent deck immersion. Deck immersion is a serious problem which can cause a ship to sink.

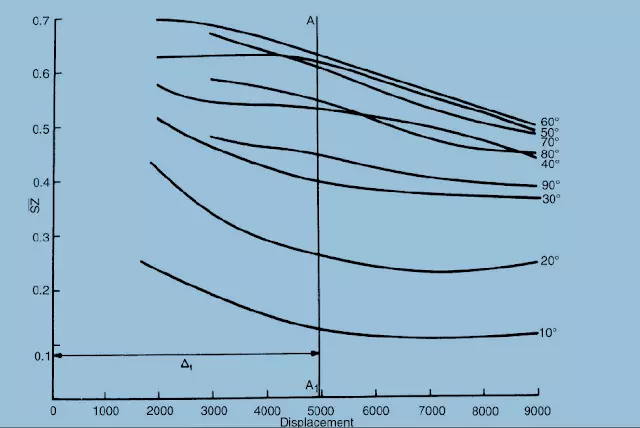
CROSS CURVES OF STABILITY 

Due to varying loading on ship, the centre of gravity keeps on changing. Also with loading or unloading, displacement changes. As the value of GZ curves changes with displacement of the ship, it is tedious to draw it for each displacement value. SZ curves makes the task much easier. If we take any arbitrary fixed point S the perpendicular distance SZ with respect to line of action, A set of following curves are obtained.

Figure 6: Stability Cross Curves

From the curves as it is seen, at a particular displacement Value of SZ is found out for various angles of heel. These could be put into the following formula and GZ could easily be found out.

GZ = SZ + SGsinθ,

             SG=distance between the arbitrary point S and Centre of Gravity G. 

SZ curves only depends upon the geometry of the ship and hence can be drawn

during the design phase.

If we consider the case of an Aircraft carrier, it can have a good amount of flare so as to

perform well in rough waves, and its pitching motion have to be considered. These type of ships pitch and roll simultaneously so as to maintain stability. While if we take an large Cargo Carrier or a ship with tumblehome, the waterplane area is very large so there is very small pitching.

There much more criteria for stability with more formulas and concepts applied on different kind of ships to gain stability and control over the ships. However, we limit our discussion to the basic concepts without delving deeper. Stability is a big pastureland in oceans and our venture into a vessel's performance is incomplete without it. 

It is not just related to a set of mathematical interpretations but the physics behind it and its applicability in all types of ship operations is of pivotal character. We would come up with our next article related to the precise detailing of the practices carried out often in vessels to reduce risk of heeling due to free surface effects and careless loading-unloading operations.