Involute Curve

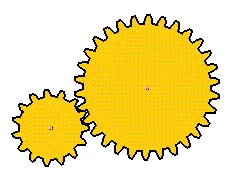
The following examples are involute spur gears. We use the word involute because the contour of gear teeth curves inward. Gears have many terminologies, parameters and principles. One of the important concepts is the velocity ratio, which is the ratio of the rotary velocity of the driver gear to that of the driven gears.

The SimDesign file for these gears is simdesign/gear15.30.sim. The number of teeth in these gears are 15 and 30, respectively. If the 15-tooth gear is the driving gear and the 30-teeth gear is the driven gear, their velocity ratio is 2.

Other examples of gears are in simdesign/gear10.30.sim and simdesign/gear20.30.sim

Generation of the Involute Curve

Figure 7-3 Involute curve

The curve most commonly used for gear-tooth profiles is the involute of a circle. This involute curve is the path traced by a point on a line as the line rolls without slipping on the circumference of a circle. It may also be defined as a path traced by the end of a string which is originally wrapped on a circle when the string is unwrapped from the circle. The circle from which the involute is derived is called the base circle.

In Figure 7-3, let line MN roll in the counterclockwise direction on the circumference of a circle without slipping. When the line has reached the position M'N', its original point of tangent A has reached the position K, having traced the involute curve AK during the motion. As the motion continues, the point A will trace the involute curve AKC.

Properties of Involute Curves

  1. The distance BK is equal to the arc AB, because link MN rolls without slipping on the circle.
  2. For any instant, the instantaneous center of the motion of the line is its point of tangent with the circle.
    Note: We have not defined the term     instantaneous center previously. The instantaneous center or instant center is defined in two ways (Bradford & Guillet 43):
    1. When two bodies have planar relative motion, the instant center is a point on one body about which the other rotates at the instant considered.
    2. When two bodies have planar relative motion, the instant center is the point at which the bodies are relatively at rest at the instant considered.
  3. The normal at any point of an involute is tangent to the base circle. Because of the property (2) of the involute curve, the motion of the point that is tracing the involute is perpendicular to the line at any instant, and hence the curve traced will also be perpendicular to the line at any instant.
  4. There is no involute curve within the base circle.