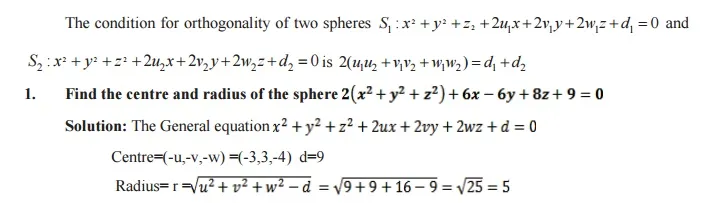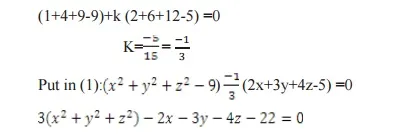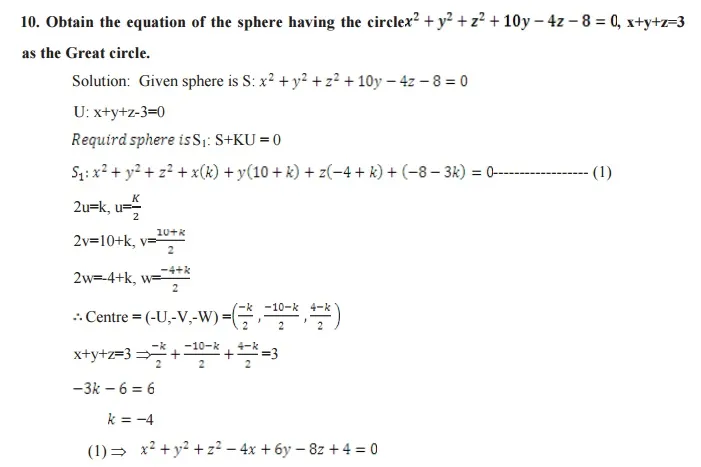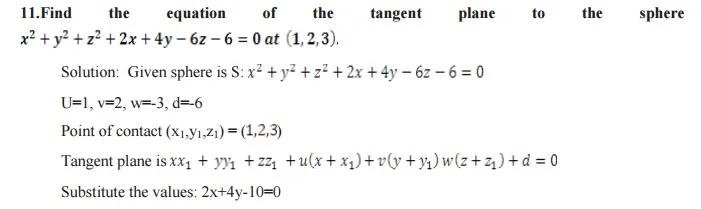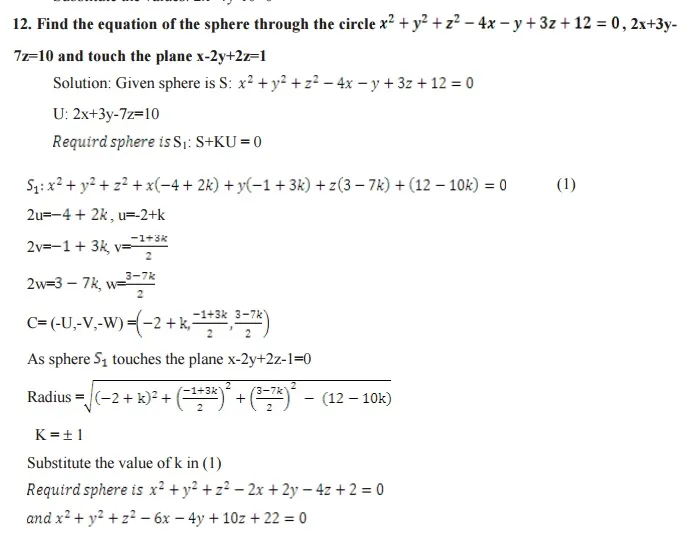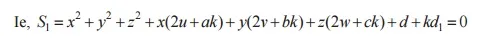
THE SPHERE
DEFINITION: A sphere is the locus of a point moving at a constant distance form a fixed point. The constant distance is the radius and the fixed point is the centre of the sphere.
PLANE SECTION OF A SPHERE:
A plane section of a sphere is a circle sphere S: x2+y2+z2+2ux+2vy+2wz+d=0 plane U: ax+by+cz+d1= 0 the combined equation (S,U) is a circle.
The equation of the sphere through the circle a (S, U ) is S1=S+KU
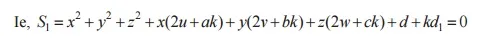
EQUATION OF THE TANGENT PLANE
The sphere is x2+y2+z2+2ux+2vy+2wz+d=0 and the point of contact is (x1,y1,z1) then Equation of the Tangent plane is xx1+yy1+zz1+ u(x+x1)+v(y+y1)+w(z+z1) +d=0
CONDITION FOR TANGENCY:
Condition for tangency is perpendicular from centre to the plane = radius
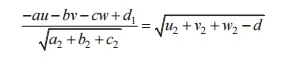
CONDITION FOR ORTHOGONALITY OF TWO SPHERES:
The condition for orthogonality of two spheres