Integral Calculus

Introduction

Gottfried Wilhelm Leibnitz (1646-1716) and Sir Isaac Newton (1643-1727) independently discovered calculus in the mid-17th century. Leibnitz, a German philosopher, mathematician, and political adviser, importantly both as a metaphysician and as a logician, was a distinguished independent inventor of the Differential and Integral Calculus. Sir Isaac Newton had created an expression for the area under a curve by considering a momentary increase at a point.

In effect, the fundamental theorem of calculus was built into his calculations. His work and discoveries were not limited to mathematics; he also developed theories in optics and gravitation.

One cannot imagine a world without differentiation and integration. In this century, we witnessed remarkable scientific advancement owing to the ingenious application of these two basic components of Mathematics. Calculus serve as unavoidable tool for finding solutions to the variety of problems that arise in physics, astronomy, engineering, chemistry, geology, biology, and social sciences.

Calculus deals principally with two geometric problems.

(i) The problem of finding SLOPE of the tangent line to the curve, is studied by the limiting process known as differentiation and

(ii) Problem of finding the AREA of a region under a curve is studied by another limiting process called Integration.

In chapters 9 and 10, we have studied the differential calculus. In this chapter let us study some fundamentals of integration.

Consider some simple situations illustrated below.

Situation 1

The shortest distance between two points A and B in a plane is the line segment joining the straight line A and B. Suppose it is required to find the line connecting two points A and B that do not lie on a vertical line such that a moving particle slides down on this line from A to B in the shortest time (minimum time). Most of us believe that the shortest distance path in Fig. 11.1(a) will take the shortest time.

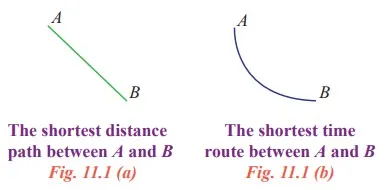
Certainly this route is not the shortest time route joining the points A and B, because the velocity of the motion in the straight line (Fig. 11.1(a)) will be comparatively slow; whereas it take a curve that is steeper near A (Fig. 11.1(b)), even though the path becomes longer, a considerable portion of the distance will be covered at a greater speed. The solution to this problem is solved by Integral calculus. This is called Brachistochrone problem which initiates the study of calculus of variation using integral tool.

Situation 2

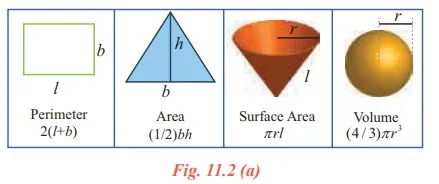
In elementary geometry we have learnt to evaluate the measure of the following regular shape of the figures given below by using known formulae.

How can the measure of the following figures given by functions be calculated?

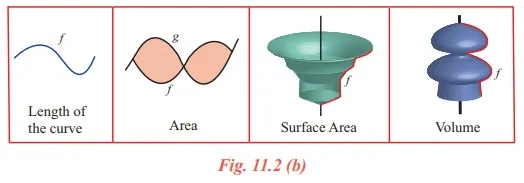
Though the problems look so difficult, integral calculus solves it without any difficulties.

Situation 3

At a particular moment, a student needs to stop his speedy bike to avoid a collision with the barrier ahead at a distance 40 metres away from him. Immediately he slows (acceleration) down the bike applying brake at a rate of 8 meter/second² . If the bike is moving at a speed of 24m/s, when the brakes are applied, will it stop before collision?

Also look at the following problems that occur naturally in our life.

• What speed has to be applied to fire a satellite upward so that it never returns to the earth? • What is the radius of the smallest circular disk that can cover every isosceles triangle of given perimeter P? • What volume of material is removed from a solid sphere of radius 2r if a hole of radius r is drilled through the centre? • If a strain of bacteria grows at a rate proportional to the amount present and if the population doubles in one hour, how much will it increase at the end of two hours? Integration will answer for all the above problems.