
Lagrange Multipliers
In the previous section we optimized (i.e. found the absolute extrema) a function on a region that contained its boundary. Finding potential optimal points in the interior of the region isn’t too bad in general, all that we needed to do was find the critical points and plug them into the function. However, as we saw in the examples finding potential optimal points on the boundary was often a fairly long and messy process.
In this section we are going to take a look at another way of optimizing a function subject to given constraint(s). The constraint(s) may be the equation(s) that describe the boundary of a region although in this section we won’t concentrate on those types of problems since this method just requires a general constraint and doesn’t really care where the constraint came from.
So, let’s get things set up. We want to optimize (i.e. find the minimum and maximum value of) a function, f(x,y,z) subject to the constraint (x,y,z)=k. Again, the constraint may be the equation that describes the boundary of a region or it may not be. The process is actually fairly simple, although the work can still be a little overwhelming at times.


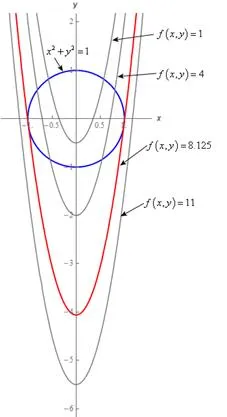

.




