Finding Maxima and Minima using Derivatives

Where is a function at a high or low point? Calculus can help!

A maximum is a high point and a minimum is a low point:

In a smoothly changing function a maximum or minimum is always where the function flattens out  (except for a saddle point).

Where does it flatten out?  Where the slope is zero.

Where is the slope zero?  The Derivative tells us!

Let's dive right in with an example:

 How Do We Know it is a Maximum (or Minimum)?

We saw it on the graph! But otherwise ... derivatives come to the rescue again.

Take the derivative of the slope (the second derivative of the original function):

The Derivative of 14 − 10t is −10

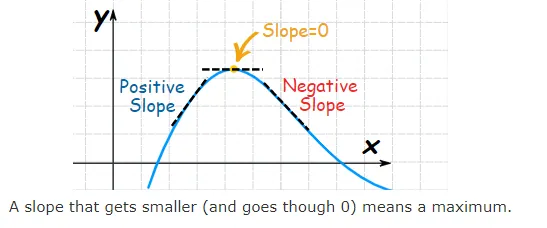
This means the slope is continually getting smaller (−10): travelling from left to right the slope starts out positive (the function rises), goes through zero (the flat point), and then the slope becomes negative (the function falls):

A slope that gets smaller (and goes though 0) means a maximum.

This is called the Second Derivative Test

On the graph above I showed the slope before and after, but in practice we do the test at the point where the slope is zero:

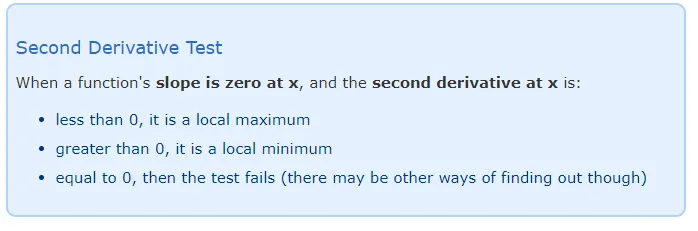
"Second Derivative: less than 0 is a maximum, greater than 0 is a minimum"

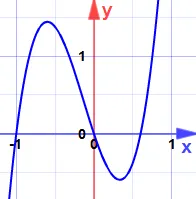
 Example: Find the maxima and minima for:

y = 5x³ + 2x² − 3x

The derivative (slope) is:

y = 15x² + 4x − 3

Which is quadratic with zeros at:

·         x = −3/5

·         x = +1/3 

Could they be maxima or minima? (Don't look at the graph yet!)

 The second derivative is y'' = 30x + 4

At x = −3/5:

y'' = 30(−3/5) + 4 = −14

it is less than 0, so −3/5 is a local maximum

At x = +1/3:

y'' = 30(+1/3) + 4 = +14

it is greater than 0, so +1/3 is a local minimum

(Now you can look at the graph.)