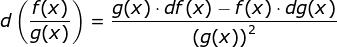
Quotient Rule

Definition and Formula

The quotient rule is a formula for taking the derivative of a quotient of two functions. It makes it somewhat easier to keep track of all of the terms. Let's look at the formula.

If you have function f(x) in the numerator and the function g(x) in the denominator, then the derivative is found using this formula:

In this formula, the d denotes a derivative. So, df(x) means the derivative of function f and dg(x) means the derivative of function g. The formula states that to find the derivative of f(x) divided by g(x), you must:

1. Take g(x) times the derivative of f(x).
2. Then from that product, you must subtract the product of f(x) times the derivative of g(x).
3. Finally, you divide those terms by g(x) squared.

Mnemonic Device

The quotient rule formula may be a little difficult to remember. Perhaps a little yodeling-type chant can help you. Imagine a frog yodeling, 'LO dHI less HI dLO over LO LO.' In this mnemonic device, LO refers to the denominator function and HI refers to the numerator function.

Let's translate the frog's yodel back into the formula for the quotient rule.

LO dHI means denominator times the derivative of the numerator: g(x) times df(x).

less means 'minus'.

HI dLO means numerator times the derivative of the denominator: f(x) times dg(x).

over means 'divide by'.

LO LO means take the denominator times itself: g(x) squared.

Examples

Let's look at a couple of examples where we have to apply the quotient rule.

In the first example, let's take the derivative of the following quotient:

Let's define the functions for the quotient rule formula and the mnemonic device. The f(x) function (the HI) is x^3 - x+ 7. The g(x) function (the LO) is x^2 - 3.

Now, let's take the derivative of each function. df(x), or dHI, is 3x^2 - 1. dg(x), or dLO, is 2x.