Law of Gearing

Consider the portions of the two teeth, one on the wheel 1 (or pinion) and the other on the wheel 2. Let the two teeth come in contact at point Q, and the wheels rotate in the directions as shown in the figure.

Let T T be the common tangent and MN be the common normal to the curves at the point of contact Q. From the centres O₁ and O₂, draw O₁M and O₂N perpendicular to MN. A little consideration will show that the point Q moves in the direction QC, when considered as a point on wheel 1, and in the direction QD when considered as a point on wheel 2.

Let v₁ and v₂ be the velocities of the point Q on the wheels 1 and 2 respectively. If the teeth are to remain in contact, then the components of these velocities along the common normal MN must be equal.

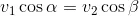
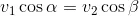
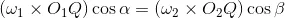
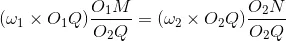
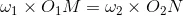
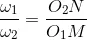
Also from similar triangles O₁MP and O₂NP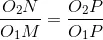

Combining equations we have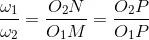

From above, we see that the angular velocity ratio is inversely proportional to the ratio of the distances of the point P from the centers O₁ and O₂, or the common normal to the two surfaces at the point of contact Q intersects the line of centers at point P which divides the center distance inversely as the ratio of angular velocities.

Therefore in order to have a constant angular velocity ratio for all positions of the wheels, the point P must be the fixed point (called pitch point) for the two wheels. In other words, the common normal at the point of contact between a pair of teeth must always pass through the pitch point. This is the fundamental condition which must be satisfied while designing the profiles for the teeth of gear wheels. It is also known as law of gearing.