D'Alembert's principle

D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert. It is the dynamic analogue to the principle of virtual work for applied forces in a static system and in fact is more general than Hamilton's principle, avoiding restriction to holonomic systems. A holonomic constraint depends only on the coordinates and time. It does not depend on the velocities. If the negative terms in accelerations are recognized as inertial forces, the statement of d'Alembert's principle becomes The total virtual work of the impressed forces plus the inertial forces vanishes for reversible displacements.The principle does not apply for irreversible displacements, such as sliding friction, and more general specification of the irreversibility is required.

The principle states that the sum of the differences between the forces acting on a system of mass particles and the time derivatives of the momenta of the system itself projected onto any virtual displacement consistent with the constraints of the system is zero. Thus, in symbols d'Alembert's principle is written as following,

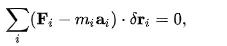
This above equation is often called d'Alembert's principle, but it was first written in this variational form by Joseph Louis Lagrange.[4] D'Alembert's contribution was to demonstrate that in the totality of a dynamic system the forces of constraint vanish. That is to say that the generalized forces {\displaystyle {\mathbf {Q} }_{j}} need not include constraint forces. It is equivalent to the somewhat more cumbersome Gauss's principle of least constraint.

General case with changing masses