Conditions for Static Equilibrium
We say that a rigid body is in equilibrium when both its linear and angular acceleration are zero relative to an inertial frame of reference. This means that a body in equilibrium can be moving, but if so, its linear and angular velocities must be constant. We say that a rigid body is in static equilibrium when it is at rest in our selected frame of reference. Notice that the distinction between the state of rest and a state of uniform motion is artificial—that is, an object may be at rest in our selected frame of reference, yet to an observer moving at constant velocity relative to our frame, the same object appears to be in uniform motion with constant velocity. Because the motion is relative, what is in static equilibrium to us is in dynamic equilibrium to the moving observer, and vice versa. Since the laws of physics are identical for all inertial reference frames, in an inertial frame of reference, there is no distinction between static equilibrium and equilibrium.
According to Newton’s second law of motion, the linear acceleration of a rigid body is caused by a net force acting on it, or

Here, the sum is of all external forces acting on the body, where m is its mass and →aCMa→CM is the linear acceleration of its center of mass (a concept we discussed in Linear Momentum and Collisions on linear momentum and collisions). In equilibrium, the linear acceleration is zero. If we set the acceleration to zero in (Figure), we obtain the following equation:
The first equilibrium condition for the static equilibrium of a rigid body expresses translational equilibrium:
The first equilibrium condition, (Figure), is the equilibrium condition for forces, which we encountered when studying applications of Newton’s laws.
This vector equation is equivalent to the following three scalar equations for the components of the net force:
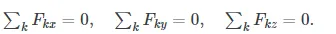
Analogously to (Figure), we can state that the rotational acceleration →αα→ of a rigid body about a fixed axis of rotation is caused by the net torque acting on the body, or
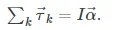
Here II is the rotational inertia of the body in rotation about this axis and the summation is over all torques →τkτ→k of external forces in (Figure). In equilibrium, the rotational acceleration is zero. By setting to zero the right-hand side of (Figure), we obtain the second equilibrium condition:
The second equilibrium condition for the static equilibrium of a rigid body expresses rotational equilibrium:
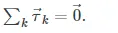
The second equilibrium condition, (Figure), is the equilibrium condition for torques that we encountered when we studied rotational dynamics. It is worth noting that this equation for equilibrium is generally valid for rotational equilibrium about any axis of rotation (fixed or otherwise). Again, this vector equation is equivalent to three scalar equations for the vector components of the net torque:
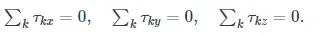
The second equilibrium condition means that in equilibrium, there is no net external torque to cause rotation about any axis.
In the final step in this chain of reasoning, we used the fact that in equilibrium in the old frame of reference, S, the first term vanishes because of (Figure) and the second term vanishes because of (Figure). Hence, we see that the net torque in any inertial frame of reference S′S′ is zero, provided that both conditions for equilibrium hold in an inertial frame of reference S.
The practical implication of this is that when applying equilibrium conditions for a rigid body, we are free to choose any point as the origin of the reference frame. Our choice of reference frame is dictated by the physical specifics of the problem we are solving. In one frame of reference, the mathematical form of the equilibrium conditions may be quite complicated, whereas in another frame, the same conditions may have a simpler mathematical form that is easy to solve. The origin of a selected frame of reference is called the pivot point.
In the most general case, equilibrium conditions are expressed by the six scalar equations ((Figure) and (Figure)). For planar equilibrium problems with rotation about a fixed axis, which we consider in this chapter, we can reduce the number of equations to three. The standard procedure is to adopt a frame of reference where the z-axis is the axis of rotation. With this choice of axis, the net torque has only a z-component, all forces that have non-zero torques lie in the xy-plane, and therefore contributions to the net torque come from only the x– and y-components of external forces. Thus, for planar problems with the axis of rotation perpendicular to the xy-plane, we have the following three equilibrium conditions for forces and torques:
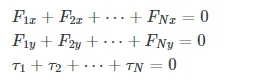
where the summation is over all N external forces acting on the body and over their torques. In (Figure), we simplified the notation by dropping the subscript z, but we understand here that the summation is over all contributions along the z-axis, which is the axis of rotation. In (Figure), the z-component of torque 
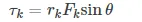


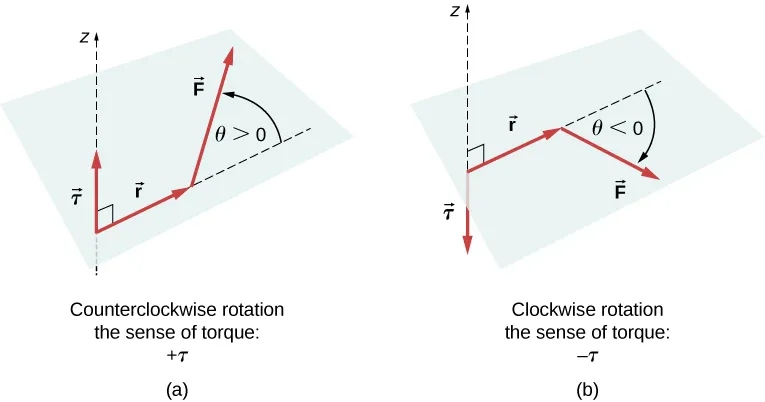
Figure 12.2 Torque of a force: (a) When the torque of a force causes counterclockwise rotation about the axis of rotation, we say that its sense is positive, which means the torque vector is parallel to the axis of rotation. (b) When torque of a force causes clockwise rotation about the axis, we say that its sense is negative, which means the torque vector is antiparallel to the axis of rotation.
View this demonstration to see two forces act on a rigid square in two dimensions. At all times, the static equilibrium conditions given by (Figure) through (Figure) are satisfied. You can vary magnitudes of the forces and their lever arms and observe the effect these changes have on the square.
In many equilibrium situations, one of the forces acting on the body is its weight. In free-body diagrams, the weight vector is attached to the center of gravity of the body. For all practical purposes, the center of gravity is identical to the center of mass, as you learned in Linear Momentum and Collisions on linear momentum and collisions. Only in situations where a body has a large spatial extension so that the gravitational field is nonuniform throughout its volume, are the center of gravity and the center of mass located at different points. In practical situations, however, even objects as large as buildings or cruise ships are located in a uniform gravitational field on Earth’s surface, where the acceleration due to gravity has a constant magnitude of g=9.8m/s2. In these situations, the center of gravity is identical to the center of mass. Therefore, throughout this chapter, we use the center of mass (CM) as the point where the weight vector is attached. Recall that the CM has a special physical meaning: When an external force is applied to a body at exactly its CM, the body as a whole undergoes translational motion and such a force does not cause rotation.
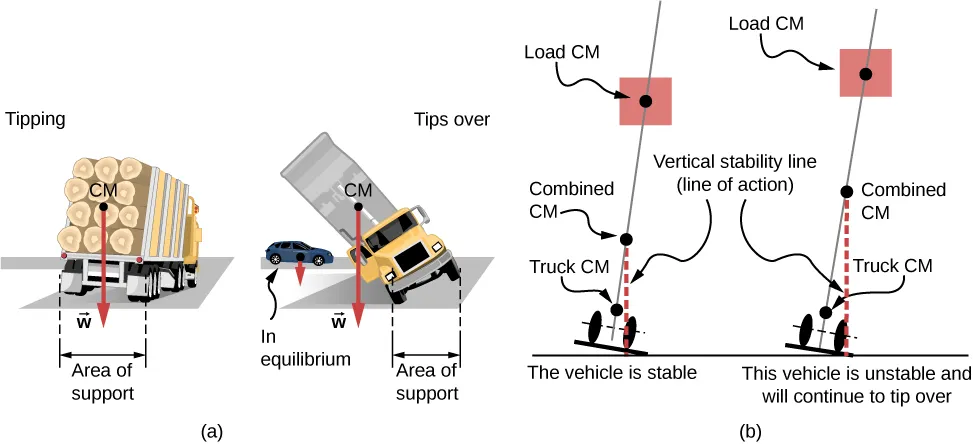
When the CM is located off the axis of rotation, a net gravitational torque occurs on an object. Gravitational torque is the torque caused by weight. This gravitational torque may rotate the object if there is no support present to balance it. The magnitude of the gravitational torque depends on how far away from the pivot the CM is located. For example, in the case of a tipping truck ((Figure)), the pivot is located on the line where the tires make contact with the road’s surface. If the CM is located high above the road’s surface, the gravitational torque may be large enough to turn the truck over. Passenger cars with a low-lying CM, close to the pavement, are more resistant to tipping over than are trucks.

Figure 12.3 The distribution of mass affects the position of the center of mass (CM), where the weight vector →ww→ is attached. If the center of gravity is within the area of support, the truck returns to its initial position after tipping [see the left panel in (b)]. But if the center of gravity lies outside the area of support, the truck turns over [see the right panel in (b)]. Both vehicles in (b) are out of equilibrium. Notice that the car in (a) is in equilibrium: The low location of its center of gravity makes it hard to tip over.
If you tilt a box so that one edge remains in contact with the table beneath it, then one edge of the base of support becomes a pivot. As long as the center of gravity of the box remains over the base of support, gravitational torque rotates the box back toward its original position of stable equilibrium. When the center of gravity moves outside of the base of support, gravitational torque rotates the box in the opposite direction, and the box rolls over. View this demonstration to experiment with stable and unstable positions of a box.