Constrained Motion and Constraint Forces

Constrained motion results when an object is forced to move in a restricted way. For example, it may have to move along a curved track, to slide on a table that may accelerate upwards, to stay in contact with an accelerating wedge, etc.

Constraint Forces are the forces that the constraining object exerts on the object to make it follow the motional constraints.

In this module and in the next one, we will consider multi-object systems where the constraint forces will make the objects in the system to move with the same acceleration in magnitude and direction.

Constraints on a Single Point Particle

Imagine a box resting on the horizontal floor of an elevator at rest. The box interacts with the Earth and the elevator's floor. The resulting forces are the gravitational force pulling down and the normal force pushing up. The free body diagram is simple and shown at the right of the figure below:

This situation has all the hallmarks of constrained motion: The requirement that the object remain on the floor requires that it's y-component of acceleration equal that of the floor (in this case is zero). This in turn requires the normal force to have a particular value. In this situation, the normal force is the constraint force.

Constraint Forces adjust themselves according to Newton's Second Law so that the acceleration of an object is just the right value for the object to follow the motion required by the particular constrained.

Typical Constraint Forces

§  Normal Forces

§  Tension in an ideal rope

§  Static friction (as long as slipping does not begin).

§  An external force that causes a particular motion (e.g. car has acceleration A due to attached rocket)

Constraints in Systems with Multiple Objects

Imagine the previous situation with an additional box stacked on top of the box on the elevator's floor. The elevator is accelerating upwards with an acceleration of magnitude a. Now it is clear that the motion of the upper box is constrained by the motion of the lower box. Both boxes have the same acceleration (a_u,y = a_l,y), and as before, the lower box is moving with the same acceleration as the elevator (a_l,y = a).

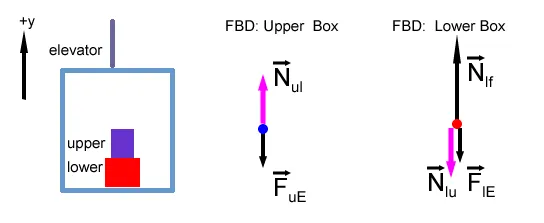
In this example, the normal forces resulting from the interaction between both boxes and the normal force due to the interaction between the lower box and the elevator's floor constrain both boxes to move with the elevator's acceleration:

a_u,y = a _l,y = a

The normal forces, shown in the free body diagram above, are the constraint forces. They will adjust their magnitudes according to Newton's second law to provide the proper acceleration to both boxes. Note: N_ul and N_lu are Newton's 3^rd law pair, and are therefore drawn with the same magnitude.

Calculate the normal forces

Given the masses of the upper and lower boxes, m_u and m_l, we can find the three normal forces for a given elevator's acceleration 'a'. For that purpose we will first consider two separate systems, one containing only the upper box, the other one containing only the lower box. Later we will discuss considering both boxes as the system.

1. Two Separate systems

The force diagrams of each box are shown again in the following figure. The equations below each of the force diagrams are the vertical component of Newton's second law written consistently with a coordinate system with the vertical y - axis positive upwards.

Note that for each system we have two independent equations, (eq.1) and (eq. 2), with 5 unknowns:

§  the three normal forces (N_ul, N_lf and N_lu), and

§  the box's accelerations, a_l,y and a_u,y.

Because the motion of the boxes is constrained to move together with the elevator provide us with two extra equations: a_l,y = a and a_u,y = a, (eq. 3 and 4). The last equation needed is the equality of the magnitudes of the contact forces between boxes which are Newton's third law pairs (eq. 5 in the figure).

The normal force on the upper box due to the lower one is:

N_ul = m_u(g + a)

and, the normal force on the lower box due to the floor is:

N_lf = (m_l+m_u)(g + a)

2. Combined System: upper box + lower box

The above expression of the normal force exerted on the lower box by the floor, N_lf, makes sense. If we think that both boxes are constrained to move with the same acceleration, then both boxes can be treated as a system consisting of a point particle of total mass (m_u + m_l) moving under the action of the gravitational force acting on the total mass and the external normal force exerted on the lower box by the floor. To justify this approach we first identify the interactions and classify the resulting forces:

Then we calculate the net force acting on the system using to find that:

The free body diagram of the of the combined 'upper-lower boxes' system is shown below.

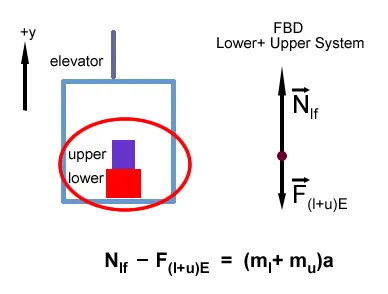
Now the procedure to solve for the normal force exerted on the lower box by the floor is the same as the one we followed to answer the first concept question in this module. We start by writing Newton's second law for the system as shown below the free body diagram. Note that only the external forces appear in the terms of the net force. The signs on each term of the equation are consistent with a y-axis positive upwards. Using in this equation that the gravitational force on the combined system is F_(l+u)E = (m_u+m_l)g, we recover the same result obtained by considering two independent systems:

N_lf = (m_l+m_u)(g + a)

In the combined system, the normal forces between the boxes are now internal forces and they are not included in the free body diagram of the combined system. As mentioned in the previous module this cancellation is fundamentally a result of the constraint imposed by Newton's Third Law. The internal forces come in opposing pairs and cancel. Because of this cancellation, we say that internal forces are irrelevant to the acceleration of the system. Only the external forces, in this case the gravitational on the system and the normal on the lower box by the floor, will contribute to the acceleration of the system.

The advantage of considering the combined system is that it is the most straightforward way to calculate the external normal force N_lf. On the other hand, it does not provide any information about the internal contact force, N_ul. For that purpose we must consider a system for which this force is an external force: the upper box.