
Buoyancy and Floatation: Differences, Problems and Solutions
1. Meaning of Buoyancy:
Consider a body immersed in a liquid. Consider an elemental vertical cylinder of the body of height y and sectional area da. Let the intensity of pressure on the top end of the cylinder be p. The intensity of pressure on the bottom of the cylinder will be (p + wy).

Hence we find that, when a body is immersed in a liquid, the liquid will exert an upward force on the body equal to the weight of the liquid displaced by the body. This upward force exerted by the liquid on the body is called the Force of Buoyancy or Upthrust. This principle is called Archimedes’ Principle of Buoyancy.
Since the force of Buoyancy is a vertical force and equal to the weight of the liquid displaced by the body, the point of action of the buoyant force is the centre of gravity of the liquid displaced. This point of action of the buoyant force is called the centre of buoyancy.
2. Body Immersed in Two Different Fluids:
Fig. 4.9 shows a body of volume V immersed in two different fluids of specific weights w1 and w2 respectively.
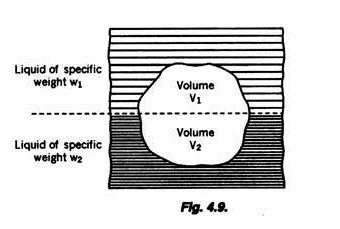
In this case the upthrust on the body = Weight of the volume V1 of liquid of specific weight of w1 + Weight of volume V2 of the liquid of specific weight w2 where V1 and V2 are the volumes of the two liquids displaced by the body.
∴ Upthrust = w1 V1 + w2 V2
= Total weight of the liquids displaced by the body.
3. Metacentre and Metacentric Height of a Floating Body:
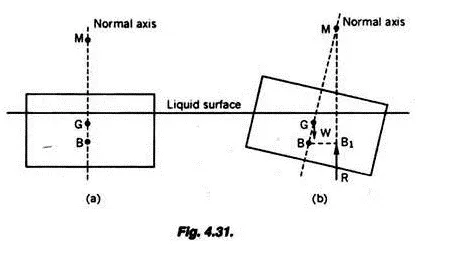
Fig. 4.31. (a) shows a body floating in a liquid and in equilibrium. Let G be the centre of gravity of the body and B be the centre of buoyancy. Obviously B and G lie on the same vertical. Suppose now the body is given a tilt by a small angle as shown in Fig. 4.31 (b). The centre of buoyancy will now shift to a new position B1. The upthrust will now be an upward force through B1.
The line of action of the upthrust in this new position will intersect the normal axis of the body at a point say M. This point M is called the metacentre.
This is the point at which the line of action of the upthrust will meet the normal axis of the body when the body is tilted by a small angle. The distance MG between the metacentre and the centre of gravity of the body is called the metacentric-height.
4. Conditions of Equilibrium of a Floating Body:
(i) When a body is floating in a liquid, the weight of the body is equal to the weight of the liquid displaced.
(ii) When the metacentre is above the centre of gravity as in Fig. 4.31, we find, on giving a small tilt to the floating body, the weight of the body and the upthrust will form a Righting couple i.e. a restoring couple to bring the body back to its position. The body is, therefore, said to be in stable equilibrium.
(iii) When the metacentre is below the centre of gravity as in Fig. 4.32, we find on giving a small tilt to the floating body, the weight of the body and the upthrust will make the body tilt further and the body will not therefore be restored to its earlier position. In this case the body is said to be in unstable equilibrium.
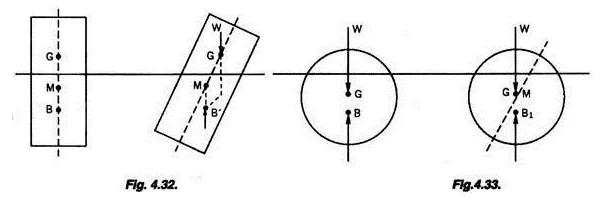
(iv) When the metacentre and the centre of gravity coincide, the body will remain in equilibrium in any position in which it is floating. See Fig. 4.33.
If the body is tilted, it will remain in equilibrium in the new position, since in the new position also the weight of the body and the upthrust will remain in the same vertical. A body floating in this way is said to be in Neutral equilibrium.
5. To Determine the Metacentric Height of a Floating Body:
The position of the metacentre with respect to the position of the centre of buoyancy can be determined as follows.
Let a floating body (Fig. 4.34) heel by a small angle θ in a clockwise direction. The immersed section has now changed from abcd to a1 b1 cd. Consequently let the centre of buoyancy change from B to B1.
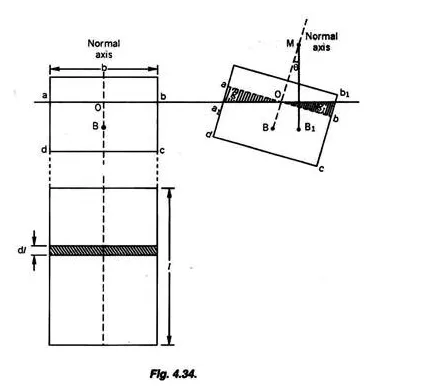
It may be realized that the effect of heeling is to move an immersed wedge of water aoa1 to the position bob1. This apparent movement of this wedge has resulted in shifting the centre of buoyancy from B to B1.


6. Experimental Determination of the Metacentric Height:
Let W be the weight of a floating ship.
Let a known weight m be placed on one side of the ship.
A simple pendulum consisting of a heavy weight suspended by a long cord is placed in the ship and the position of the bob of the pendulum is noted.
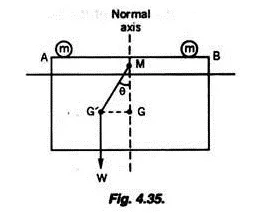
Let l be the length of the simple pendulum. Now the weight m is made to move from the position A to the position B. Let this displacement be x. Since the string of the pendulum will remain plumb, the angle of heel θ can be measured by the apparent deflection of the pendulum.

Ships carry considerable quantities of water for boilers, and running prime movers etc. This water is stored in the lower region of the ship. Water stored in a ship in this manner is called Bilge water or Ballast water. When a ship slightly tilts, the shape of the bilge water will change and the centre of buoyancy of the whole ship will also be shifted accordingly.
The displacement of the centre of gravity of the bilge water may affect the stability of the ship adversely. As the bilge water shifts its position the metacentric heights of the ship will be considerably changed. To maintain the stability of the ship it is better to provide the bilge water in separate compartments instead of providing it as one huge mass of water.
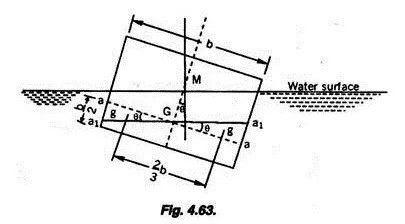
Consider the floating rectangular pontoon shown in Fig. 4.63. Let the pontoon contain a certain quantity of bilge water at its bottom. Let aa be the original surface of bilge water. Let the pontoon be subjected to a small angle of heel θ. In the new position the bilge water surface is represented by a1 a1.
The effect of the heel is to move a wedge of bilge water from one side of the pontoon to another, accordingly the centre of gravity of the pontoon and its contents will also be shifted.
The relation-
