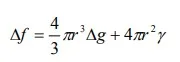
Kinetics of nucleation and growth

Structural changes in metallic systems usually take place by nucleation and growth whether it is just a phase change within one of the three states, or a simple structural rearrangement within a single phase, or a phase transformation. An equilibrium phase diagram presents the phases and phase changes expected under equilibrium conditions, but it provides no information about the rates of transformation. Although changes in pressure, composition, or temperature can cause phase transformations, it is temperature changes that are more important. From a micro structural standpoint, the first process to accompany a phase transformation is nucleation (i.e. the formation of very small particles or nuclei of the product phase from the parent phase) of the new phase particles which are capable of growing. The second stage is growth, in which the nucleated particles increase their size. The transformation reaches completion if growth of these new phase particles is allowed to proceed until the equilibrium fraction is attained.

Both nucleation and growth require that the accompanying free energy change be negative. Consequently, the super-heating or super-cooling that is necessary for a phase change is to be expected. That is a transformation cannot tale place precisely at the equilibrium transformation temperature because at that temperature free energies of phases are equal. In addition to temperature, two other factors that affect transformation rate – first, diffusion controlled rearrangement of atoms because of compositional and/or crystal structural differences; second, difficulty encountered in nucleating small particles via change in surface energy associated with the interface. Diffusion limits both the nucleation and growth rates in many cases.

With the nucleation of new particle, new interface is created between the particle and liquid. This interface will have positive energy that must be supplied during the transformation process. A tiny particle has a large surface area to volume ratio and therefore be unstable. Thus energy of the surface can effectively prevent the initial formation of a tiny particle. A particle said to have nucleated when it becomes stable and will not disappear due to thermal fluctuations. After a particle attained a critical size, it can grow further with a continuous decrease in energy. The surface energy is no longer a dominant factor in the growth process.

Nucleation kinetics

In homogeneous nucleation, the probability of nucleation occurring at any given site is identical to that at any other site within the volume of the parent phase. When a pure liquid metal is cooled below its equilibrium freezing temperature to a sufficient degree, numerous homogeneous nuclei are created by slow-moving atoms bonding together. Homogeneous nucleation usually requires a considerable amount of undercooling (cooling a material below the equilibrium temperature for a given transformation without the transformation occurring). Undercooling enhances the formation of nuclei that eventually grow. If ∆f is the free energy change accompanying the formation of a spherical new phase particle,

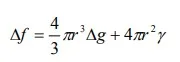
where r is the radius of the particle, ∆g is the Gibbs free energy change per unit volume and γ is the surface energy of the interface. As surface energy, γ, is always positive, and ∆g is negative, passes through a maximum. From calculus, critical values can be found from the following:

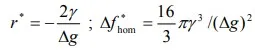
Particles which are smaller than the critical size are called embryos; those larger than the critical size are called nuclei. As ∆g becomes more negative with a lowering of the temperature, the critical values of ∆f and r becomes smaller as shown in figure-12. At sufficiently low temperatures, nucleation can be triggered by a few atoms statistically clustering as a nucleus, so a small critical radius is exceeded. With added growth, the new phase attains stability. Of course atom movements are sluggish at low temperatures, so growth is generally slow.

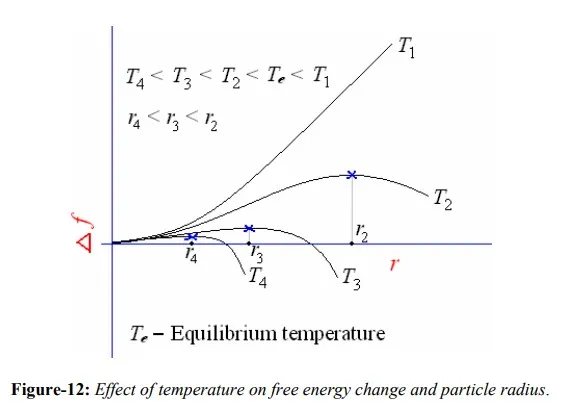
The greater the degree of undercooling below the equilibrium melting temperature of the metal, the greater the change in volume free energy, however, the change in free energy due to surface energy does not change much with temperature. Thus, the critical size of nuclei is mainly determined by volume free energy. Near the freezing temperature, critical nucleus size must be infinite since ∆T approaches zero. As the amount of undercooling increases, critical size decreases, and are related as follows:

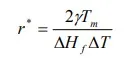
where T_m – freezing temperature (in K), ∆H_f – latent heat of fusion, ∆T – amount of undercooling at which nucleus is formed.

In heterogeneous nucleation, the probability of nucleation occurring at certain preferred sites is much greater than that at other sites. During solidification, inclusions of foreign particles (inoculants), walls of container holding the liquid provide preferred sites. Irregularities in crystal structure such as point defects and dislocations possess strain energy. In solid-solid transformation, foreign inclusions, grain boundaries, interfaces, stacking faults and dislocations can act as preferred sites for nucleation as the strain energy associated with them will be reduced. The released strain energy can reduce the energy requirements for free energy change, ∆f. Therefore, nucleation proceeds with a smaller critical radius. A majority of reactions are initiated by some type of heterogeneous nucleation which is common among the two types.

For example, consider the nucleation of β from α occurring on a foreign inclusion, δ, as shown in figure-13. Considering the force equilibrium in surface tension terms,

where θ is the contact angle. An expression for ∆f can be written in terms of volume energy and surface energies as follows:

By comparing the free energy terms for homogeneous and heterogeneous nucleation processes for various contact conditions:

The above derivations are helpful in selecting a heterogeneous nucleation agent. It shows that a small contact angle is very helpful in heterogeneous nucleation. For a system of α – β interface, θ can be minimized by choosing δ such that energy of β- δ interface is kept to minimum. If the crystal structure two phases are similar and their lattice parameters are nearly equal, energy of the interface between those two phases will be minimum. This criterion is useful in selecting a agent for heterogeneous nucleation.

Growth kinetics

Many transformations occur as a result of continuous formation of critical nuclei in the parent phase and the subsequent growth of the particles. Growth is the increase in size of the particle after it has nucleated i.e. growth kinetics become important once an embryo has exceeded the critical size and become a stable nucleus. Growth may proceed in two radically different manners. In one type of growth, individual atoms move independently from the parent to the product phase, thus it is diffusion controlled and is thermally activated. In the other type of growth that occurs in solid-solid transformations many atoms move cooperatively without thermal assistance. Growth that is diffusion controlled is more common the other.

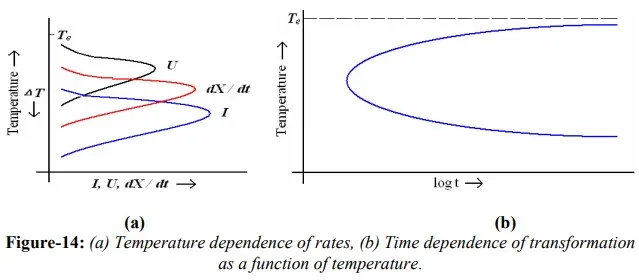
Growth usually occurs by the thermally activated jump of atoms from the parent phase to the product phase. The unit step in the growth process thus consists of an atom leaving the parent phase and jumping across the interface to join the product phase. At the equilibrium temperature, both phases have the same free energy, hence the frequency of jumps from parent phase to product phase will be equal to that from product phase to parent phase i.e. the net growth rate is zero. At lower temperatures, product phase is expected to have lower free energy, and thus a net flow of atoms from parent phase to product phase. This net flux of atoms results in interface motion i.e. growth rate is taken as the rate of increase of a linear dimension of a growing particle. As a function of temperature, the growth rate first increases with increasing degree of supercooling, but eventually slows-down as thermal energy decreases. This is same as for nucleation; however the maximum in the growth rate usually occurs at a higher temperature than the maximum in the nucleation rate. Figure-14(a) depicts the temperature dependence of nucleation rate (U), growth rate (I) and overall transformation rate (dX/dt) that is a function of both nucleation rate and growth rate i.e. dX/dt= fn (U, I). On the other-hand, the time required for a transformation to completion has a reciprocal relationship to the overall transformation rate. Temperature dependence of this time is shown in figure-14 (b). The C-curve shown in figure-14(b) is characteristic of all thermally activated nucleation and growth transformations involving the transformation of a hightemperature phase to low-temperature phase. This curve is also known as timetemperature-transformation (TTT) curve. The nose of the C-curve corresponds to the minimum time for a specified fraction of transformation. It is also the place where overall transformation rate is a maximum.

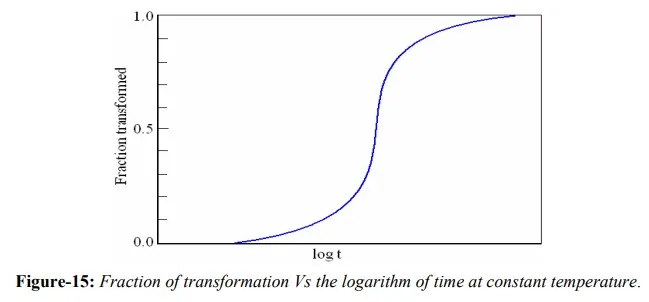
In many investigations, the fraction of transformation that has occurred is measured as a function of time, while the temperature is maintained constant. Transformation progress is usually ascertained by either microscopic examination or measurement of some physical property. Transformation data are plotted as the fraction of transformed material versus the logarithm of time, which results in characteristic S-curve (figure-15), largely because diffusion plays such an important role in both nucleation and growth. Conditions under which transformation may take place greatly affect the nature of the resulting microstructure. At small degrees of supercooling, where slow nucleation and rapid growth prevail, relatively coarse particles appear; at larger degrees of supercooling, relatively fine particles result. The time dependence of the transformation rate is an important consideration in the heat treatment of materials.

The other kind of growth involves congruent transformation which is considered as diffusion-less because it takes place at a rate approaching the speed of sound. It can be visualized as a cooperative type of process in which, without aid of thermal activation, atoms move into new locations because of the strain energy resulting from like movements of adjacent atoms. However the strains set-up in the parent phase may impede the further transformation, thus a lower temperature or mechanical deformation may be required to complete this martensitic transformation. The cooperative displacement of atoms here resembles a shear process during which, for example, FCC structure of Co transforms into HCP-Co or FCC-austenite into BCT-martensite. This merely requires that atoms in the FCC-phase move a fraction of an inter-atomic distance.

Because of its crystallographic nature, a martensitic transformation only occurs in the solid state. In addition, the crystal structure of the product phase must be easily generated from that of the parent phase without diffusive motion of atoms. This is true for most allotropic transformations in metals that occur at low temperatures or for hightemperature transformations of metals brought about by a quench. Reasons for martensitic transformation: (a) the free energy difference between the high-temperature phase and low-temperature phases becomes increasingly negative with decreasing temperature (b) the crystal structures of allotropes of a metal are relatively simple and share similar features with each other. It is also said that diffusion-controlled nucleation and growth and a martensitic change are competitive processes in many cases.

The martensitic transformation starts at a temperature designated Ms, which is generally below the equilibrium temperature, T_e. The transformation is completed at a lower temperature, M_f. The amount of parent phase transformed into product phase depends on temperature only, and is independent of time. Furthermore, in most cases, Ms temperature and the fractional amount of product phase as a function of temperature are independent of quenching rate. Consequently, M_s and M_f are presented as horizontal lines on a TTT diagram. Catalytic effect of cold working can be used to make Ms approach T_e. Martensitic transformations in Fe-C alloys and T_i are of great technological importance. Fe-C alloy transformations are dealt in detail in the following sections.