Reduction of systematic errors

The prerequisite for the reduction of systematic errors is a complete analysis of the measurement system that identifies all sources of error. Simple faults within a system, such as bent meter needles and poor cabling practices, can usually be readily and cheaply rectified once they have been identified. However, other error sources require more detailed analysis and treatment. Various approaches to error reduction are considered below.

Careful instrument design

Careful instrument design is the most useful weapon in the battle against environmental inputs, by reducing the sensitivity of an instrument to environmental inputs to as low a level as possible. For instance, in the design of strain gauges, the element should be constructed from a material whose resistance has a very low temperature coefficient (i.e. the variation of the resistance with temperature is very small). However, errors due to the way in which an instrument is designed are not always easy to correct, and a choice often has to be made between the high cost of redesign and the alternative of accepting the reduced measurement accuracy if redesign is not undertaken.

Method of opposing inputs

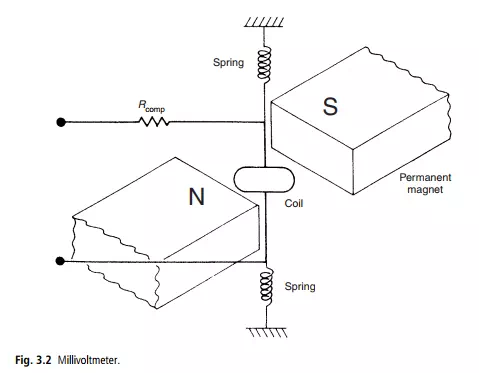
The method of opposing inputs compensates for the effect of an environmental input in a measurement system by introducing an equal and opposite environmental input that cancels it out. One example of how this technique is applied is in the type of millivoltmeter shown in Figure 3.2. This consists of a coil suspended in a fixed magnetic field produced by a permanent magnet. When an unknown voltage is applied to the coil, the magnetic field due to the current interacts with the fixed field and causes the coil (and a pointer attached to the coil) to turn. If the coil resistance Rcoil is sensitive to temperature, then any environmental input to the system in the form of a temperature change will alter the value of the coil current for a given applied voltage and so alter the pointer output reading. Compensation for this is made by introducing a compensating resistance Rcomp into the circuit, where Rcomp has a temperature coefficient that is equal in magnitude but opposite in sign to that of the coil. Thus, in response to an increase in temperature, Rcoil increases but Rcomp decreases, and so the total resistance remains approximately the same.

High-gain feedback

The benefit of adding high-gain feedback to many measurement systems is illustrated by considering the case of the voltage-measuring instrument whose block diagram is shown in Figure 3.3. In this system, the unknown voltage Ei is applied to a motor of torque constant Km, and the induced torque turns a pointer against the restraining action of a spring with spring constant Ks. The effect of environmental inputs on the

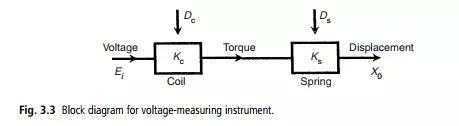
motor and spring constants is represented by variables Dm and Ds. In the absence of environmental inputs, the displacement of the pointer X0 is given by: X0 D KmKsEi. However, in the presence of environmental inputs, both Km and Ks change, and the relationship between X0 and Ei can be affected greatly. Therefore, it becomes difficult or impossible to calculate Ei from the measured value of X0. Consider now what happens if the system is converted into a high-gain, closed-loop one, as shown in Figure 3.4, by adding an amplifier of gain constant Ka and a feedback device with gain constant Kf. Assume also that the effect of environmental inputs on the values of Ka and Kf are represented by Da and Df. The feedback device feeds back a voltage E0 proportional to the pointer displacement X0. This is compared with the unknown voltage Ei by a comparator and the error is amplified. Writing down the equations of the system, we have:

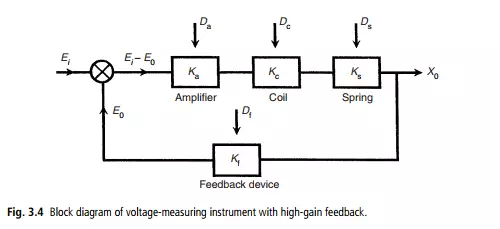
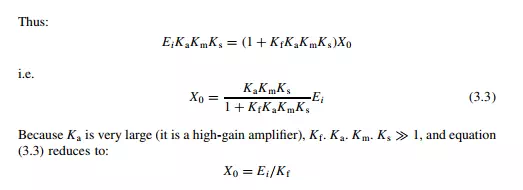
This is a highly important result because we have reduced the relationship between X0 and Ei to one that involves only Kf. The sensitivity of the gain constants Ka, Km and Ks to the environmental inputs Da, Dm and Ds has thereby been rendered irrelevant, and we only have to be concerned with one environmental input Df. Conveniently, it is usually easy to design a feedback device that is insensitive to environmental inputs: this is much easier than trying to make a motor or spring insensitive. Thus, highgain feedback techniques are often a very effective way of reducing a measurement system’s sensitivity to environmental inputs. However, one potential problem that must be mentioned is that there is a possibility that high-gain feedback will cause instability in the system. Therefore, any application of this method must include careful stability analysis of the system.