Analog Filters

A filter can be defined with reference to various fields such as chemistry, optics, engineering, turbulence modelling, engineering, computing, philosophy, and signal processing. Let us consider signal processing filters, filter can be defined as a device used for removing unnecessary part or parts of the signal. This removing of unnecessary parts of the signal is called as filtering process. These signal processing filters are classified into various types such as electronic filters, digital filters, and analog filters.

Analog Filters

Analog filter is typically used in electronics and is considered as a basic building block of signal processing. These analog filters are used to separate audio signals before applying to loudspeakers. To separate and to combine several telephone conversations onto a single channel can be done using analog filters. To select a particular radio station from the radio receiver by rejecting all other channels can be done using analog filters. The continuously varying signals (analog signals) can be operated using passive linear electronic analog filters which are composed of passive elements such as resistors, capacitors, and inductors. These analogue filters are frequently used for allowing particular frequency components by rejecting other from analog or continuous time signals.

Types of Analog Filters

The linear analog filters can be listed as network synthesis filters, image impedance filters, and simple filters. The network synthesis filters are again classified as a Butterworth filter, Chebyshev filter, Elliptic filter or Cauer filter, Bessel filter, Gaussian filter, Optimum ‘L’ filter (Legendre), and Linkwithz-Riley filter. The image impedance filters are further classified as a Constant k filter, m-derived filter, general image filters, Zobel network, lattice filter, bridged T delay equalizer, composite image filter, and mm’-type filter. The RC filter, RL filter, LC filter, and RLC filter are called as simple filters.

Analog Filter Design

The analog filter design includes analog filter transfer functions, poles and zeros of analog filters, frequency response of analog filters, output response, and different types of analog filters. The analog filter design filter methods are classified as Butterworth, Chebyshev, and Elliptic filter models based transfer function with order ‘n’.

Butterworth Filter

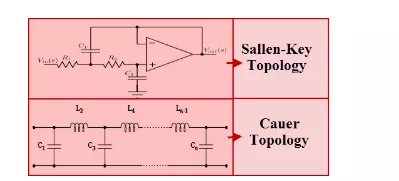
Butterworth Filter Design

The Butterworth or maximally flat magnitude filter has a flat (mathematically as much as possible) frequency response. The analog low pass filter’s (Butterworth) ‘brick wall’, which can be defined as standard approximations for various filter orders are shown in the below figure (including ideal frequency response).

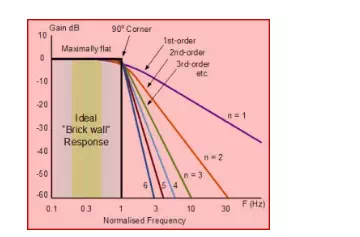
Butterworth Filter Ideal Frequency Response

If we increase the order of the Butterworth filter, then the Butterworth filter design cascaded stages also gets increased. Thus, as shown in the above figure the filter and brick wall response gets closer. Generally, the linear analog filters are realized using various topologies, the Butterworth filter can be realized using Cauer topology or Sallen-key topology.

Chebyshev Filter

The Chebysev filters are named after Pafnufy Chebyshev who derived the mathematical calculations of Chebyshev filters. The error between the characteristic of idealized filter and actual filter can be reduced using the property of Chebyshev filter.

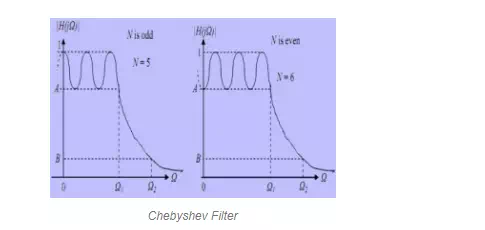
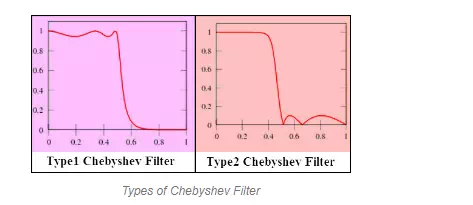
These Chebyshev filters are further classified as type1 and type2 Chebyshev filters. The type1 filters are basic type and the gain or amplitude response is an angular frequency function of the nth order of analog low pass filter (LPF-if we consider analog filters). The type2 Chebyshev filter is an uncommon type and is an inverse filter.

Simple Analog Filters

RC-Filter

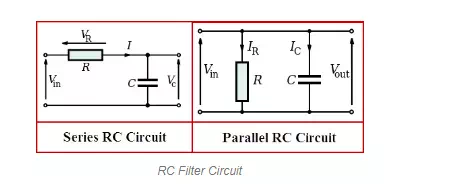
The simple resistor-capacitor electric circuits driven by current or voltage source acts as analog filters. These RC filter circuits are used for filtering a signal such that they block specific frequencies and allows other frequencies to pass. The RC filter circuit can be connected as series RC circuit or parallel RC circuit as shown in the above figure.

LC-Filter

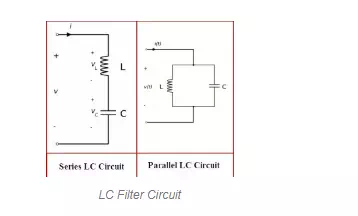
The simple inductor-capacitor electric circuit acts as an LC filter which is also termed as tuned circuit or resonant circuit or tank circuit. This LC circuit also behaves like an electrical resonator. The LC circuits are used to generate signals or to pick up signals at a specific frequency. The LC filter can be connected as series LC circuit or parallel LC circuit as shown in the above figure.

RL-Filter

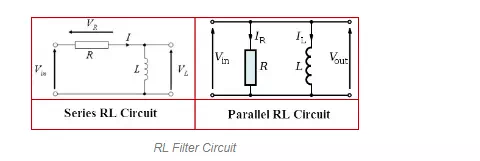
The simple resistor-inductor-capacitor electric circuit acts as an RLC filter circuit, the resistor, capacitor, and inductor can be connected in series or parallel to form series RLC-filter or parallel RLC-filter. This RLC filter circuit forms as harmonic oscillator for current and resonates like an LC circuit. But, here the oscillations can be decayed by introducing a resistor and this effect is termed as damping.