Bipolar Junction Transistor (BJT)
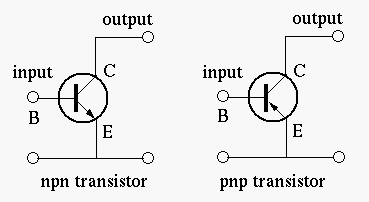
A Bipolar Junction Transistor (BJT) has three terminals connected to three doped semiconductor regions. In an NPN transistor, a thin and lightly doped P-type base is sandwiched between a heavily doped N-type emitter and another N-type collector; while in a PNP transistor, a thin and lightly doped N-type base is sandwiched between a heavily doped P-type emitter and another P-type collector. In the following we will only consider NPN BJTs.
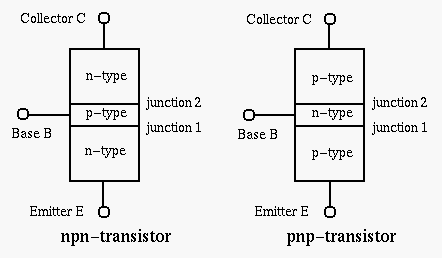
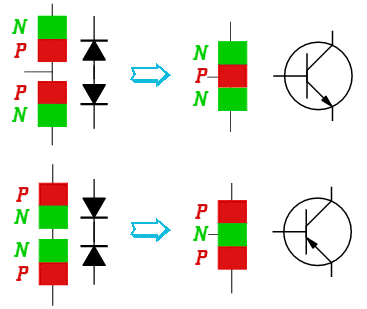
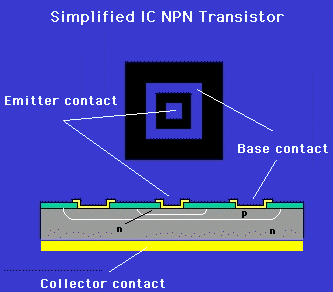
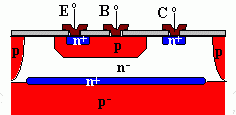
In many schematics of transistor circuits (especially when there exist a large number of transistors in the circuit), the circle in the symbol of a transistor is omitted. The figures below show the cross section of two NPN transistors. Note that although both the collector and emitter of a transistor are made of N-type semiconductor material, they have totally different geometry and therefore can not be interchanged.
All previously considered components (resistor, capacitor, inductor, and diode) have two terminals (leads) and can therefore be characterized by the single relationship between the current going through and the voltage across the two leads. Differently, a transistor is a three-terminal component, which could be considered as a two-port network with an input-port and an output-port, each formed by two of the three terminals, and characterized by the relationships of both input and output currents and voltages. Depending on which of the three terminals is used as common terminal, there can be three possible configurations for the two-port network formed by a transistor:
- Common emitter (CE),
- Common base (CB),
- Common collector (CC).
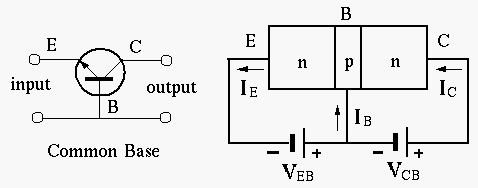
- Common-Base (CB) configuration
Two voltages ![]() and
and ![]() are applied respectively to the
emitter
are applied respectively to the
emitter ![]() and collector
and collector ![]() , with respect to the common base
, with respect to the common base ![]() , so that the BE junction is forward biased
while the CB junction is reverse biased.
, so that the BE junction is forward biased
while the CB junction is reverse biased.
Note that the polarity of ![]() and direction of
and direction of ![]() associated with the PN-junction
between E and B are the same as those associated with a diode, voltage
polarity: positive on P, negative on N, current direction: from P to N,
but
associated with the PN-junction
between E and B are the same as those associated with a diode, voltage
polarity: positive on P, negative on N, current direction: from P to N,
but ![]() and the direction of
and the direction of ![]() associated with the PN-junction
between the base and collector are defined oppositely.
associated with the PN-junction
between the base and collector are defined oppositely.
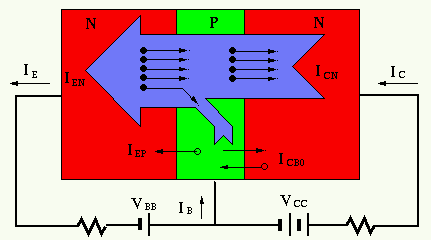
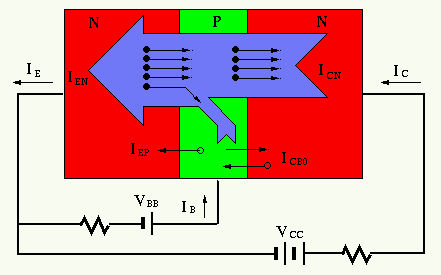
The behavior of the NPN-transistor is determined by its two PN-junctions:
- The
forward biased base-emitter (BE) PN-junction allows the free electrons in
emitter to go through the PN-junction to arrive at the base, forming the
emitter current
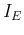 .
. - As
the P-type base is thin and lightly doped, only a small number of the
electrons from the emitter are combined with the holes in base to form
the base current
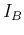 .
. - Most of the electrons coming from the emitter become minority carriers in the P-type base, and they go through the reverse biased collector-base PN junction to arrive at the collector.
- The
percentage of those electrons that arrive at the collector out of the
electrons from the emitter is defined as
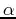 (e.g.,
(e.g., 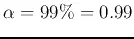 , depending on the
doping and geometry of the material). The total collector current
, depending on the
doping and geometry of the material). The total collector current 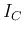 is therefore
is therefore 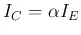 .
.
The current gain or current transfer
ratio is defined as the ratio between the emitter (input)
current ![]() and the collector (output)
current
and the collector (output)
current ![]() :
:
![]()
The base current ![]() is:
is:
![]()
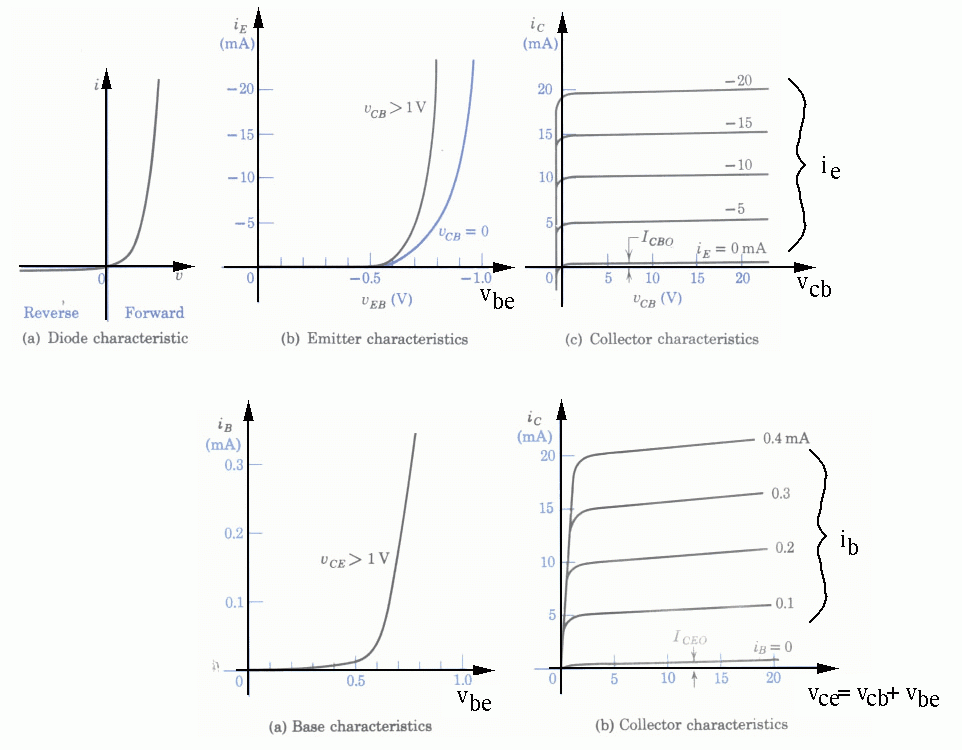
- The CB configuration can be considered as a 2-port circuit. The input port is formed by the emitter and base, the output port is formed by the collector and base. The relationships between the current and voltage of both the input and output ports are described by the following input and output characteristics.
- Input characteristics:
The input current ![]() is a
function of
is a
function of ![]() as
well as the input voltage
as
well as the input voltage ![]() , which is
much more dominant:
, which is
much more dominant:
![]()
where
![]()
This relationship between ![]() and
and ![]() as the EB junction is very
similar to the relationship of
as the EB junction is very
similar to the relationship of ![]() and
and ![]() of a diode. Also, we also note
higher
of a diode. Also, we also note
higher ![]() can slightly increase
can slightly increase ![]() .
.
- Output characteristics:
The output current ![]() is a
function of the output voltage
is a
function of the output voltage ![]() as
well as the input current
as
well as the input current ![]() , which is
much more dominant:
, which is
much more dominant:
![]()
Here the approximation is based on the assumption that ![]() (in linear region).
As
(in linear region).
As ![]() , i.e., the CB junction is
reverse biased, the current
, i.e., the CB junction is
reverse biased, the current ![]() depends
totally on
depends
totally on ![]() . When
. When ![]() ,
, ![]() is the current caused by
the minority carriers crossing the PN-junction. This is similar to the diode
current-voltage characteristics seen before, except both axes are reversed (the
polarity of
is the current caused by
the minority carriers crossing the PN-junction. This is similar to the diode
current-voltage characteristics seen before, except both axes are reversed (the
polarity of ![]() and
the direction
and
the direction ![]() are
oppositely defined). When
are
oppositely defined). When ![]() is
increased,
is
increased, ![]() is
increased correspondingly. Higher
is
increased correspondingly. Higher ![]() can
slightly increase
can
slightly increase ![]() . As
. As ![]() , CB configuration does
not have current-amplification effect. However, if
, CB configuration does
not have current-amplification effect. However, if ![]() is held constant,
is held constant, ![]() and therefore
and therefore ![]() will also be held constant, i.e.,
CB transistor circuit can be used as a current source.
will also be held constant, i.e.,
CB transistor circuit can be used as a current source.
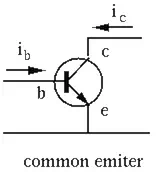
- Common-Emitter (CE) configuration
Two voltages ![]() and
and ![]() are applied respectively to the
base
are applied respectively to the
base ![]() and collector
and collector ![]() with respect to the common
emitter
with respect to the common
emitter ![]() . As
typically
. As
typically ![]() ,
the BE junction is forward biased but the CB junction is reverse biased, same
as the CB configuration. The voltages of CB and CE configurations are related
by:
,
the BE junction is forward biased but the CB junction is reverse biased, same
as the CB configuration. The voltages of CB and CE configurations are related
by:
![]()
The base current ![]() is
treated as the input current, and the collector current
is
treated as the input current, and the collector current ![]() is treated as the output
current:
is treated as the output
current:
![]()
Solving this equation for ![]() , we get the relationship between the
output
, we get the relationship between the
output ![]() and the input
and the input ![]() :
:
![]()
where we have defined the CE current gain, the ratio
of the output current ![]() and the
input current
and the
input current ![]() :
:
![]()
The two parameters ![]() and
and ![]() are related by any of the
following:
are related by any of the
following:
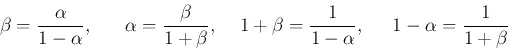
For example, if ![]() ,
then
,
then ![]() .
.
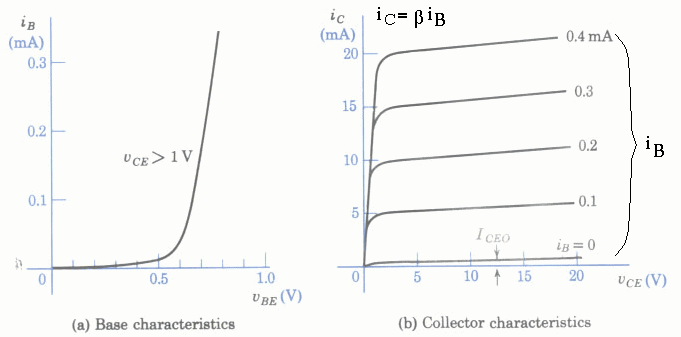
The CE configuration can be considered as a 2-port circuit. The input port is formed by the base and emitter, the output port is formed by the collector and emitter. The relationships between the current and voltage of both the input and output ports are described by the following input and output characteristics.
- Input characteristics:
Same as in the case of common-base configuration, the EB junction of the common-emitter configuration can also be considered as a forward biased diode, the current-voltage characteristics is similar to that of a diode:
![]()
![]() has little
effect on
has little
effect on ![]() .
.
- Output characteristics:
![]()
Higher ![]() can
slightly increase
can
slightly increase ![]() .
.
The CB junction is reverse biased, the current ![]() depends on the
current
depends on the
current ![]() . When
. When ![]() ,
, ![]() , the current caused by the minority
carriers crossing the PN-junctions. When
, the current caused by the minority
carriers crossing the PN-junctions. When ![]() is increased,
is increased, ![]() is correspondingly increased
by
is correspondingly increased
by ![]() fold.
fold.
The relationship between the input and output currents of both CB and CE configurations is summarized below:
- CB
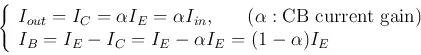
- CE
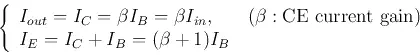
The collector characteristics of the common-base (CB) and common-emitter (CE) configurations have the following differences:
- In
CB circuit
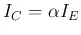 is slightly less
than
is slightly less
than 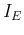 , while
in CE circuit
, while
in CE circuit 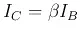 is
much greater than
is
much greater than 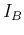 .
. - In
CB circuit,
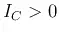 when
when 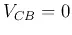 ; while in CE circuit
; while in CE circuit 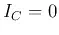 when
when 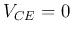 (as
(as  has the effect of
suppressing
has the effect of
suppressing 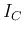 ).
). - Increased
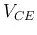 will slightly
increase
will slightly
increase 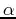 but
more greatly increase
but
more greatly increase 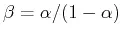 , thereby
causing more significantly increased
, thereby
causing more significantly increased 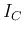 .
. 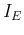 in CB is a function
of two variables
in CB is a function
of two variables 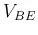 and
and 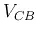 , but the former is much more
significant then the latter.
, but the former is much more
significant then the latter. 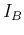 in
CE is a function of two variables
in
CE is a function of two variables 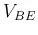 and
and 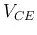 , but the former is much more
significant then the latter.
, but the former is much more
significant then the latter.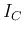 in CB is a function
of two variables
in CB is a function
of two variables 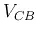 and
and 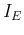 . When
. When 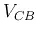 is small, its slight
increase will cause significant increase of
is small, its slight
increase will cause significant increase of 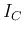 . But its further increase will not
cause much change in
. But its further increase will not
cause much change in 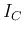 due
to saturation (all available charge carriers travel at the saturation
velocity to arrive at collector C),
due
to saturation (all available charge carriers travel at the saturation
velocity to arrive at collector C), 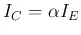 is mostly determined
by
is mostly determined
by 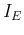 .
.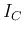 in CE is a function
of two variables
in CE is a function
of two variables 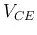 and
and 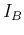 . When
. When 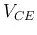 is small (
is small (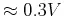 ), its slight increase will
cause significant increase of
), its slight increase will
cause significant increase of 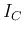 . But
when
. But
when 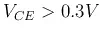 ,
its further increase will not cause much change in
,
its further increase will not cause much change in 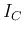 due to saturation (all
available charge carriers travel at the saturation velocity to arrive at
collector C),
due to saturation (all
available charge carriers travel at the saturation velocity to arrive at
collector C), 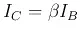 is
mostly determined by
is
mostly determined by 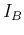 .
.
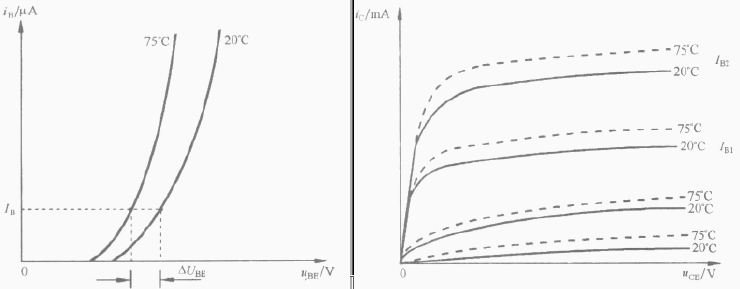
Various parameters
of a transistor change as functions of temperature. For example, ![]() increases along with temperature.
increases along with temperature.