Magnetic Materials Properties

Magnetic Materials Properties – From the magnetic point of view a material is classified according to the nature of its relative permeability (μ_r). All nonmagnetic materials are classified as paramagnetic,μ_rslightly greater than 1, and diamagnetic, μ_r slightly less than 1. For all practical purposes, μ_r of these materials can be regarded as unity, i.e. their magnetic properties are very much similar to that of free space. Such materials are not of interest to us in this treatise. Materials which are of interest to us are those whose relative permeability is much higher than that of free space. These can be classified as ferromagnetic and ferrimagnetic. Ferromagnetic materials can be further subdivided as hard and soft. Hard ferromagnetic materials include permanent magnet materials, such as alnicos, chromium steels, certain copper-nickel alloys and several other metal alloys. Soft ferromagnetic materials are iron and its alloys with nickel, cobalt, tungsten and aluminium. Silicon steels and cast steels are the most important ferromagnetic materials for use in transformers and electric machines. Ferrimagnetic materials are the ferrites and are composed of iron oxides MeO. Fe₂O₃, where Me represents a metallic ion. Ferrites are also subgrouped as hard (permanent magnetic) and soft (nickel-zinc and manganese-zinc) ferrites. Soft ferrites are quite useful in high-frequency transformers, microwave devices, and other similar high-frequency operations. There is a third category of Magnetic Materials Properties, known as superparamagnetic, made from powdered iron or other magnetic particles. These materials are used in transformers for electronics and cores for inductors. Permalloy (molybdenum-nickel-iron powder) is the best known example of this important category of magnetic materials.

Magnetic Properties of Materials

Magnetic Materials are characterized by high permeability and the nonlinear B-H relationship which exhibits both saturation and hysteresis. The physics of these properties is explained by the domain theory of magnetization usually taught in junior level courses. The B-H relationship for cyclic H is the hysteresis loop shown in Fig. 2.13 for two values of maximum flux density. It is easily observed from this figure that B is a symmetrical two-valued function of H; at any given H, B is higher if H is reducing compared to when H is increasing. This is the basic hysteresisproperty in which B lags behind H. It can also be recognized as a memory-type non-linearity in which the material remembers its previous history. Further, it is observed that the hysteresis loop becomes wider for increasing maximum flux densities. The dotted curve drawn through the positive and negative tips of the hysteresis loops with increasing maximum flux densities is the normal magnetization curve and is obtainable in virgin (unmagnetized) material by increasing the dc magnetization in either direction.

It is easily seen that because of hysteresis and saturation, the magnetic characteristic of a given material cannot be described by a few overall parameters but must be expressed in the form of a set of curves. It will be shown in Sec. 2.6 that the area of the hysteresis loop is the energy loss (it appears in the form of heat energy) per unit volume in one cycle of magnetization. This loss depends upon the quality of material and the maximum flux density at which the material is operated. Hysteresis loop as such is of little use in engineering applications except in illustrating the waveform of the exciting current. It is the normal (dc) magnetization curve which is of direct application in magnetic circuit calculationsand design. In short form it will be referred as the magnetization curve. The hysteresis loss represented by the loop area is usually lumped with the eddy-current loss (Sec. 2.6) and the two together are known as the core (or iron) loss which is parameterized by material thickness and frequency and is expressed as loss per unit volume (specific loss).

Sheet Steels

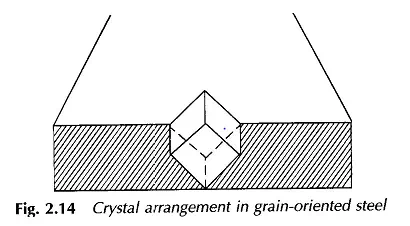
Nearly all transformers and certain parts of electric machines use silicon steel in the form of sheets, thinly insulated on each side. Silicon is added to steel to increase its resistivity thereby reducing the eddy-current loss. Building the core out of thin sheets (laminations) greatly aids in reduction of the eddy-current loss. The crystalline structure of silicon steel is body centred cubic an atom at each corner of the cube and an atom at the cube centre. The cubic structure presents considerable ease of magnetization (high μ_r) along the cube edge as compared to the diagonal on the cube side and the diagonal through the cube body which is most difficult to magnetize. Therefore, if silicon steel crystals are aligned so that the cube edges lie parallel to the direction of magnetization, the material has a much higher relative permeability and can be operated at much higher flux densities with moderate exciting currents and also has superior core-loss qualities. This crystal arrangement is illustrated in Fig. 2.14. The crystal arrangement is practically achieved by cold-rolling steel sheets. The material is then termed as cold-rolled grain-oriented steel (crgos) and is invariably employed in electromechanical devices. Annealing of silicon steel sheets further helps in proper alignment of crystals. The saturation flux density and electric resistivity are of course independent of the grain orientation.

Magnetostriction

When ferromagnetic materials are subjected to magnetizing mmf, these undergo small changes in dimensions. The lengthwise change is of the order of 10^-5 m and is accompanied by transverse changes of the opposite sign. These changes are caused by magnetostriction. Their nature is hysteric with consequent dissipation of energy when magnetization is alternating. Further, there are associated mechanical stresses which produce noise in audible bandwidth which can be a nuisance for high fluxdensities employed in transformers in modern practice. Magnetostriction noise may, therefore, be the subject of limiting specificaztions in transformers.

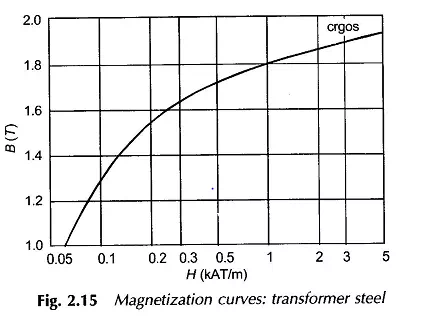
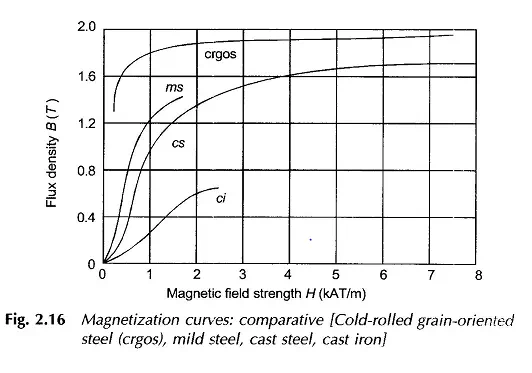
Magnetization Curves

Typical magnetization curves of transformer steel are given in Fig. 2.15 and a comparative set of magnetization curves are given in Fig. 2.16.