Octal Arithmetic

Octal Number System

Following are the characteristics of an octal number system.

· Uses eight digits, 0,1,2,3,4,5,6,7.

· Also called base 8 number system.

· Each position in an octal number represents a 0 power of the base (8). Example: 8⁰

· Last position in an octal number represents an x power of the base (8). Example: 8^x where x represents the last position - 1.

Example

Octal Number − 12570₈

Calculating Decimal Equivalent −

Step	Octal Number	Decimal Number
Step 1	125708	((1 × 8^4) + (2 × 8^3) + (5 × 8^2) + (7 × 8^1) + (0 × 8^0))10
Step 2	125708	(4096 + 1024 + 320 + 56 + 0)10
Step 3	125708	549610

Note − 12570₈ is normally written as 12570.

Octal Addition

Following octal addition table will help you to handle octal addition.

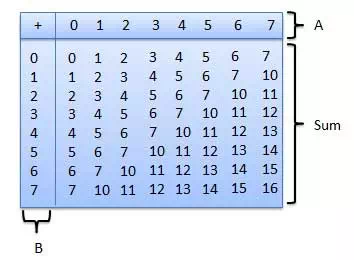
To use this table, simply follow the directions used in this example: Add 6₈and 5₈. Locate 6 in the A column then locate the 5 in the B column. The point in 'sum' area where these two columns intersect is the 'sum' of two numbers.

68 + 58 = 138.

Example − Addition

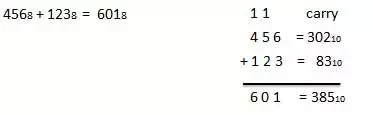
Octal Subtraction

The subtraction of octal numbers follows the same rules as the subtraction of numbers in any other number system. The only variation is in borrowed number. In the decimal system, you borrow a group of 10₁₀. In the binary system, you borrow a group of 2₁₀. In the octal system you borrow a group of 8₁₀.

Example − Subtraction

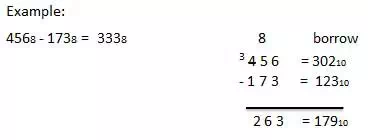
Multiplication of Octal Numbers

In multiplication of octal numbers a simple rule for multiplication of two digits in any radix is to multiply them in decimal. If the product is less than the radix, then we take it as the result. If the product is greater than the radix we divide it by the radix and take the remainder as the least significant digit. The quotient is taken as carry in the next significant digit.

For example, (3)₄ × (1)₄ = (3)₄ but (3)₄ × (2)₄ = (12)₄ since 3 × 2 = 6 is decimal and division of 6 by 4 has the remainder 2 and quotient 1.

To multiply two octal numbers we use the rule given above. The process for multiplication of octal numbers is illustrated with the help of the following examples:

Evaluate:

(i) 6₈ × 23₈

Solution: 
We have 6 × 3 = 18 in decimal, which when divided by 8 gives a remainder 2 and carry 2. Again 6 × 2 = 12 in decimal, and 12 + 2 = 14. This when divided by 8 gives a remainder 6 and a carry 1. 

Hence 68 × 238 = 1628

6 × 3 = 18 18/8 = 2 with remainder 2 → l,s,d,  6 × 2 = 12 + 2 (carry) = 14 14/8 = 1 with remainder 6.

(ii) 15₈ × 44₈

Solution: 

Since 15₈ = 7₈ + 6₈, We write

15₈ × 44₈ = (7₈ + 6₈) × 44₈ = 7₈ × 44₈ + 6₈ × 44₈

Now 7 × 44 = 374

6 × 44 = 330

Taking octal addition, we have 374₈ + 330₈ = 724₈

Hence 15₈ x 44₈ = 724₈

Octal Division :

This is my fourth article on octal arithmetic. In this article I am going to solve some examples on octal division. This is very easy task and principles and rules of division remain same.

Octal Division Examples:

To solve division examples you must know how to perform multiplication on octal numbers. I will solve examples on each case. First case in which dividend and divisor both are integers. Second case in which dividend has an octal point and divisor is an integer. Third case in which both dividend and divisor both have floating point numbers. You can check your results by using this online converter.

Example#01:6573)8÷16)8

First we make a table for 16 and it's multiples.

	Decimal	Octal
16*1	14	16
16*2	32	34
16*3	48	52
16*4	64	70
16*5	80	106
16*6	96	124

          366.4

16 ⟌6573

        52

        137

        124

          133

          124

              70

               70

               XX

Answer:366.4)8