Incompletely Specified Functions
Introduction
Incompletely specified functions, also known as can't happen conditions, is a situation that sometimes occurs when certain combinations of the variables of a function cannot occur. For these combinations we can select the value of the function to be 0 or 1; whichever leads to the more minimal solution. Related below is a situation where for certain combinations of the variables one does not care what the value of the function becomes (either 0 or 1). For these can't happen and don't care situations the Karnaugh map entry is X indicating that the particular cell can be taken either as 0 or 1.
Examples
A binary coded decimal counter, having four output lines, is connected to a logic network. It is required that the output of the network be logic 1 whenever there are two or more input lines at logic 1. Also, for the binary coded decimal number 0001, the output value is of no importance. A binary coded decimal number has values ranging from 0000 to 1001 (decimal 0 to 9) the values 1010 to 1111 (decimal 10 to 15) never occurs. Let the logic network have inputs A, B, C, D where A is connected to the most significant digit of the binary coded decimal number and D to the least significant. The output from the logic network will be:
Z = f(A, B, C, D)
= ![]() (0011,0101,0110,0111,1001)
=
(0011,0101,0110,0111,1001)
= ![]() (3,5,6,7,9).
(3,5,6,7,9).
With can't happen
conditions: (1010, 1011, 1100, 1101, 1110, 1111) = (10, 11, 12, 13, 14,
15)
and the don't care conditions: (0001)
Entering this on a
Karnaugh map:
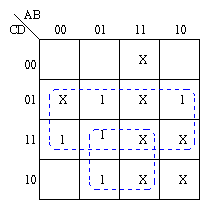
The required function is therefore: Z = f(A, B, C, D) = BC + D
ncompletely Specified Functions
- Incompletely specified function:
- Output value is not known for every combination of input variables because all combinations cannot occur.
- Truth table does not generate an output value for every possible combination of input values.
- Min-terms or max-terms that are not used as part of the output function are called don�t care terms.
Examples
Conversion of BCD to Ex-3
|
Binary |
Ex-3 |
||||||
|
W |
X |
Y |
Z |
A |
B |
C |
D |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
� |
� |
� |
� |
� |
� |
� |
� |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
Don�t care |
|||
|
1 |
0 |
1 |
1 |
Don�t care |
|||
|
� |
� |
� |
� |
� |
� |
� |
� |
|
1 |
1 |
1 |
1 |
Don�t care |
|||
A = f(w,x,y,z) = Σ(5,6,7,8,9) + Σ d(10,11,12,13,14,15)
B = f(w,x,y,z) = Σ(1,2,3,4,9) + Σ d(10,11,12,13,14,15)
C = f(w,x,y,z) = Σ(0,3,4,7,8) + Σ d(10,11,12,13,14,15)
D = f(w,x,y,z) = Σ(0,2,4,6,8) + Σ d(10,11,12,13,14,15)
- Don�t care terms can be assigned a value 0 or 1.
Rule for simplification with K-Map
Example
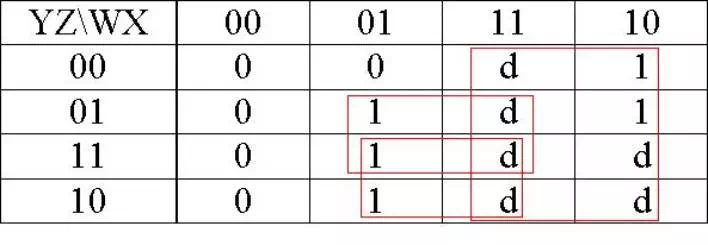
A = W + XZ + XY
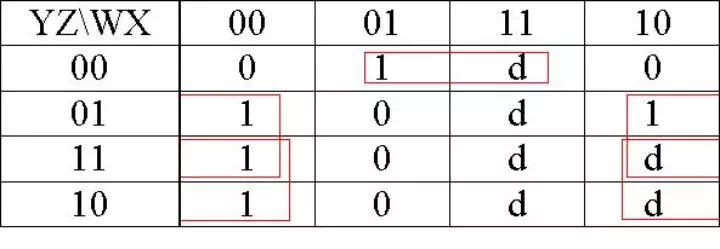
B = X�Z + X�Y + XY�Z�
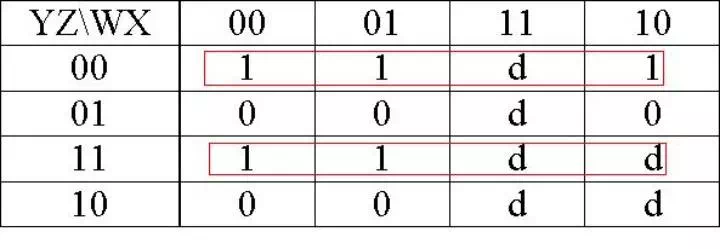
C = Y�Z� + YZ
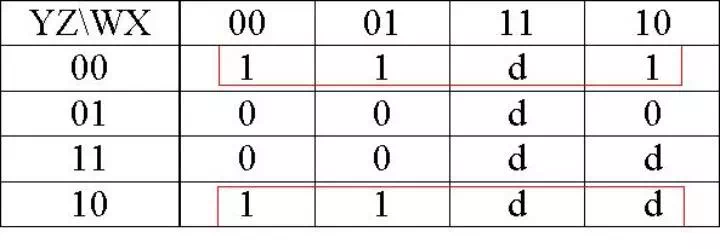
D = Z�
A = (W� * (XZ)� * (XY)�)�
B = ((X�Z)� * (X�Y)� * (XY�Z�)�)�
C = ((YZ)� * (Y�Z�)�)�
D = Z�