Error Detection & Correction Codes

What is Error?

Error is a condition when the output information does not match with the input information. During transmission, digital signals suffer from noise that can introduce errors in the binary bits travelling from one system to other. That means a 0 bit may change to 1 or a 1 bit may change to 0.

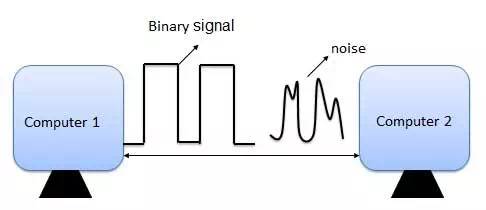
We know that the bits 0 and 1 corresponding to two different range of analog voltages. So, during transmission of binary data from one system to the other, the noise may also be added. Due to this, there may be errors in the received data at other system.

That means a bit 0 may change to 1 or a bit 1 may change to 0. We can’t avoid the interference of noise. But, we can get back the original data first by detecting whether any error(s) present and then correcting those errors. For this purpose, we can use the following codes.

• Error detection codes
• Error correction codes

Error-Detecting codes

Whenever a message is transmitted, it may get scrambled by noise or data may get corrupted. To avoid this, we use error-detecting codes which are additional data added to a given digital message to help us detect if an error occurred during transmission of the message. A simple example of error-detecting code is parity check.

Error-Correcting codes

Along with error-detecting code, we can also pass some data to figure out the original message from the corrupt message that we received. This type of code is called an error-correcting code. Error-correcting codes also deploy the same strategy as error-detecting codes but additionally, such codes also detect the exact location of the corrupt bit. In error-correcting codes, parity check has a simple way to detect errors along with a sophisticated mechanism to determine the corrupt bit location. Once the corrupt bit is located, its value is reverted (from 0 to 1 or 1 to 0) to get the original message.

How to Detect and Correct Errors?

To detect and correct the errors, additional bits are added to the data bits at the time of transmission.

· The additional bits are called parity bits. They allow detection or correction of the errors.

· The data bits along with the parity bits form a code word.

Parity Checking of Error Detection

It is the simplest technique for detecting and correcting errors. The MSB of an 8-bits word is used as the parity bit and the remaining 7 bits are used as data or message bits. The parity of 8-bits transmitted word can be either even parity or odd parity.

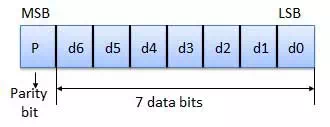
Even parity -- Even parity means the number of 1's in the given word including the parity bit should be even (2,4,6,....).

Odd parity -- Odd parity means the number of 1's in the given word including the parity bit should be odd (1,3,5,....).

Use of Parity Bit

The parity bit can be set to 0 and 1 depending on the type of the parity required.

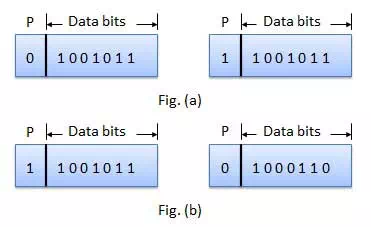
· For even parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the entire word is even. Shown in fig. (a).

· For odd parity, this bit is set to 1 or 0 such that the no. of "1 bits" in the entire word is odd. Shown in fig. (b).

How Does Error Detection Take Place?

Parity checking at the receiver can detect the presence of an error if the parity of the receiver signal is different from the expected parity. That means, if it is known that the parity of the transmitted signal is always going to be "even" and if the received signal has an odd parity, then the receiver can conclude that the received signal is not correct. If an error is detected, then the receiver will ignore the received byte and request for retransmission of the same byte to the transmitter.