DIFFERENCE BETWEEN AC AND DC:  

Current that flows continuously   in  one direction is called  direct current .  Alternating current  (A.C)  is  the  current  that  flows in  one  direction  for a  brief  time  then  reverses and flows in opposite direction for a similar time. The source for alternating current  is called a.c generator or alternator.  

Cycle:

One complete set of positive and negative values of an alternating quantity is called cycle.

Frequency:

The number of cycles made by an alternating quantity per second is called frequency. The unit of frequency is Hertz (Hz)

Amplitude or Peak value:

The maximum positive or negative value of an alternating quantity is called amplitude or peak value.

Average value:

This is the average of instantaneous values of an alternating quantity over one complete cycle of the wave.

Time period:

The time taken to complete one complete cycle.

Average value derivation:

Let i = the instantaneous value of current and i = Im sin ɵ Where, Im is the maximum value.

Resistors in series and parallel circuits:

Series circuits:

 Figure shows three resistors R1, R2 and R3 connected end to end, i.e. in series, with a battery source of V volts. Since the circuit is closed a current I will flow and the p.d. across each resistor may be determined from the voltmeter readings V1, V2 and V3

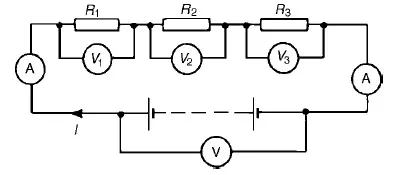
In a series circuit

 (a) the current I is the same in all parts of the circuit and hence the same reading is found on each of the two ammeters shown, and 

 (b)the sum of the voltages V1, V2 and V3 is equal to the total applied voltage, V, i.e. 

V = V1 +V2 +V3

From       Ohm’s   law:

 V1 = IR1, V2 = IR2, V3 = IR3 and V = IR where R is the total circuit resistance. Since V =V1 + V2 + V3

 then IR =IR1 + IR2 + IR3 Dividing throughout by I gives R = R1 + R2 + R3

 Thus for a series circuit, the total resistance is obtained by adding together the values of the separate resistances.

Problem 1: For the circuit shown in Figure 5.2, determine (a) the battery voltage V, (b) the total resistance of the circuit, and (c) the values of resistance of resistors R1, R2 and R3, given that the p.d.’sR1, R2acrossandR3are5V, 2V and 6V respectively.

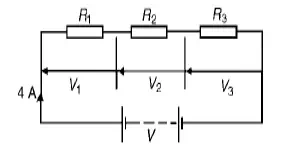
(a) Battery voltage V =V1 + V2 + V3 =5 + 2 + 6=13V

(b)Total circuit resistance R= V/ I 

= 13/4=3.25Ω

(c) Resistance R1 = V1/ I 

= 5/4

                                 =1.25 Ω Resistance R2 = V2/ I

                                 = 2/4 =0.5 Ω

                                  Resistance R3 = V3/ I = 6/4 =1.5 Ω

Problem 2. For the circuit shown in Figure determine the p.d. across resistor R3. If the total resistance of the circuit is 100_, determine the current flowing through resistor R1. Find also the value of resistor R2.

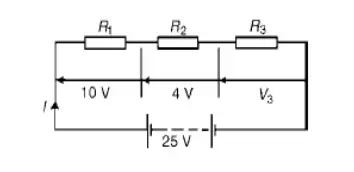
P.d. across R3, V3 =25 −10 −4=11V Current I = V/ R

 = 25/100

 =0.25A, which is the current flowing in each resistor Resistance R2 = V2/ I

 = 4/0.25 =16 Ω

Problem 3: A 12V battery is connected in a circuit having three series-connected resistors having resistances of 4 Ω, 9 Ωand 11 Ω. Determine the current flowing through, and the p.d. across the 9 Ωresistor. Find also the power dissipated in the 11 Ωresistor.

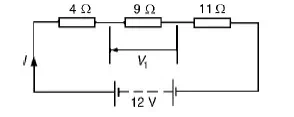
Total resistance R=4 + 9 + 11=24 Ω Current I = V/ R

 = 12/24

 =0.5A, which is the current in the 9 Ωresistor. P.d. across the 9_ resistor, V1 = I × 9 = 0.5 × 9

 = 4.5V

Power dissipated in the 11 Ωresistor, P = I2R=0.52(11)

= 0.25(11)

= 2.75W