Filters

Filters

Filters as the name suggests, they filter the frequency components. That means, they allow certain frequency components and / or reject some other frequency components.

In this chapter, let us discuss about the passive filters. Those are the electric circuits or networks having passive elements like resistor, inductor and capacitor.

Types of Filters

Filters are mainly classified into four types based on the band of frequencies that are allowing and / or the band of frequencies that are rejecting. Following are the types of filters.

Low Pass Filter
High Pass Filter
Band Pass Filter
Band Stop Filter

Low Pass Filter

Low pass filter as the name suggests, it allows (passes) only low frequencycomponents. That means, it rejects (blocks) all other high frequency components. The s-domain circuit diagram (network) of Low Pass Filter is shown in the following figure.

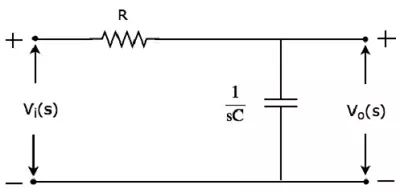
Description: Description: Low Pass Filter

It consists of two passive elements resistor and capacitor, which are connected in series. Input voltage is applied across this entire combination and the output is considered as the voltage across capacitor. Here, $V_{i} (s)$ and $V_{o} (s)$ are the Laplace transforms of input voltage, $v_{i} (t)$ and output voltage, $v_{o}$ (t) respectively.

The transfer function of the above network is

H(s)=Vo(s)Vi(s)=1sCR+1sCH(s)=Vo(s)Vi(s)=1sCR+1sC

⇒H(s)=11+sCR⇒H(s)=11+sCR

Substitute, s=jωs=jω in the above equation.

H(jω)=11+jωCRH(jω)=11+jωCR

Magnitude of transfer function is

|H(jω)|=1(1+(ωCR)2−−−−−−−−−−√|H(jω)|=1(1+(ωCR)2

· At ω = 0, the magnitude of transfer function is equal to 1.

· At $ω = \frac{1}{C R}$ , the magnitude of transfer function is equal to 0.707.

· At ω = ∞, the magnitude of transfer function is equal to 0.

Therefore, the magnitude of transfer function of Low pass filter will vary from 1 to 0 as ω varies from 0 to ∞.

High Pass Filter

High pass filter as the name suggests, it allows (passes) only high frequencycomponents. That means, it rejects (blocks) all low frequency components.

The s-domain circuit diagram (network) of High pass filter is shown in the following figure.

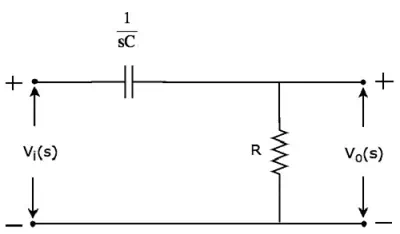
Description: Description: High Pass Filter

It consists of two passive elements capacitor and resistor, which are connected in series. Input voltage is applied across this entire combination and the output is considered as the voltage across resistor. Here, $V_{i} (s)$ and $V_{o} (s)$ are the Laplace transforms of input voltage, $v_{i} (t)$ and output voltage, $v_{o}$ (t) respectively.

The transfer function of the above network is

$ω = \frac{1}{C R}$ , the magnitude of transfer function is equal to 0.707.

· At ω = ∞, the magnitude of transfer function is equal to 1.

Therefore, the magnitude of transfer function of High pass filter will vary from 0 to 1 as ω varies from 0 to ∞.

Band Pass Filter

Band pass filter as the name suggests, it allows (passes) only one band of frequencies. In general, this frequency band lies in between low frequency range and high frequency range. That means, this filter rejects (blocks) both low and high frequency components.

The s-domain circuit diagram (network) of Band pass filter is shown in the following figure.

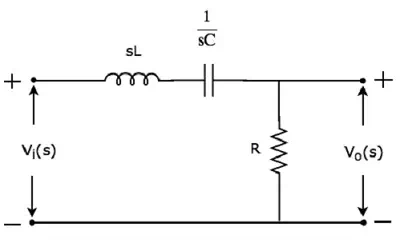
Description: Description: Band Pass Filter

It consists of three passive elements inductor, capacitor and resistor, which are connected in series. Input voltage is applied across this entire combination and the output is considered as the voltage across resistor.

Here, $V_{i} (s)$ and $V_{o} (s)$ are the Laplace transforms of input voltage, $v_{i} (t)$ and output voltage, $v_{o}$ (t) respectively.

The transfer function of the above network is

$ω = \frac{1}{\sqrt{L C}}$ , the magnitude of transfer function is equal to 1.

· At ω = ∞, the magnitude of transfer function is equal to 0.

Therefore, the magnitude of transfer function of Band pass filter will vary from 0 to 1 & 1 to 0 as ω varies from 0 to ∞.

Band Stop Filter

Band stop filter as the name suggests, it rejects (blocks) only one band of frequencies. In general, this frequency band lies in between low frequency range and high frequency range. That means, this filter allows (passes) both low and high frequency components.

The s-domain (network) of circuit diagramand stop filter is shown in the following figure.

Description: Description: Band Stop Filter

It consists of three passive elements resistor, inductor and capacitor, which are connected in series. Input voltage is applied across this entire combination and the output is considered as the voltage across the combination of inductor and capacitor.

Here, $V_{i} (s)$ and $V_{o} (s)$ are the Laplace transforms of input voltage, $v_{i} (t)$ and output voltage, $v_{o}$ (t) respectively.

The transfer function of the above network is

⇒H(s)=s2LC+1s2LC+sCR+1⇒H(s)=s2LC+1s2LC+sCR+1

Substitute, s=jωs=jω in the above equation.

H(jω)=1−ω2LC1−ω2LC+jωCRH(jω)=1−ω2LC1−ω2LC+jωCR

Magnitude of transfer function is

|H(jω)|=1−ω2LC(1−ω2LC)2+(ωCR)2−−−−−−−−−−−−−−−−−−√|H(jω)|=1−ω2LC(1−ω2LC)2+(ωCR)2

At ω = 0, the magnitude of transfer function is equal to 1.

$ω = \frac{1}{\sqrt{L C}}$ , the magnitude of transfer function is equal to 0.

· At ω = ∞, the magnitude of transfer function is equal to 1.

Therefore, the magnitude of transfer function of Band stop filter will vary from 1 to 0 & 0 to 1 as ω varies from 0 to ∞.