Coupled Circuits

Coupled Circuits

An electric circuit is said to be a coupled circuit, when there exists a mutual inductance between the coils (or inductors) present in that circuit. Coil is nothing but the series combination of resistor and inductor. In the absence of resistor, coil becomes inductor. Sometimes, the terms coil and inductor are interchangeably used. In this chapter, first let us discuss about the dot convention and then will discuss about classification of coupling.

Dot Convention

Dot convention is a technique, which gives the details about voltage polarity at the dotted terminal. This information is useful, while writing KVL equations.

· If the current enters at the dotted terminal of one coil (or inductor), then it induces a voltage at another coil (or inductor), which is having positive polarity at the dotted terminal.

· If the current leaves from the dotted terminal of one coil (or inductor), then it induces a voltage at another coil (or inductor), which is having negative polarity at the dotted terminal.

Classification of Coupling

We can classify coupling into the following two categories.

Electrical Coupling
Magnetic Coupling

Now, let us discuss about each type of coupling one by one.

Electrical Coupling

Electrical coupling occurs, when there exists a physical connection between two coils (or inductors). This coupling can be of either aiding type or opposing type. It is based on whether the current enters at the dotted terminal or leaves from the dotted terminal.

Coupling of Aiding type

Consider the following electric circuit, which is having two inductors that are connected in series.

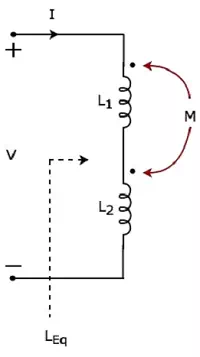
Description: Description: Coupling Aiding

Since the two inductors are connected in series, the same current I flow through both inductors having self-inductances L₁ and L₂. In this case, the current, I enter at the dotted terminal of each inductor. Hence, the induced voltage in each inductor will be having positive polarityat the dotted terminal due to the current flowing in another coil. Apply KVL around the loop of the above electric circuit or network.

$V$ =LEqdIdt

Therefore, the equivalent inductance of series combination of inductors shown in the above figure is

$L_{E q} = L_{1} + L_{2} + 2 M$

In this case, the equivalent inductance has been increased by 2M. Hence, the above electrical circuit is an example of electrical coupling which is of aidingtype.

Coupling of Opposing type

Consider the following electric circuit, which is having two inductors that are connected in series.

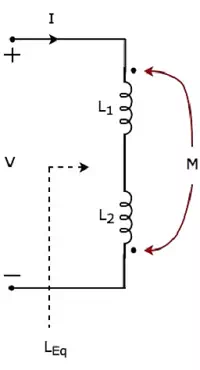
Description: Description: Coupling Opposing

In the above circuit, the current I enters at the dotted terminal of the inductor having an inductance of L₁. Hence, it induces a voltage in the other inductor having an inductance of L₂. So, positive polarity of the induced voltage is present at the dotted terminal of this inductor.

In the above circuit, the current I leaves from the dotted terminal of the inductor having an inductance of L₂. Hence, it induces a voltage in the other inductor having an inductance of L₁. So, negative polarity of the induced voltage is present at the dotted terminal of this inductor.

Apply KVL around the loop of the above electric circuit or network.

V−L1dIdt+MdIdt−L2dIdt+MdIdt=0V−L1dIdt+MdIdt−L2dIdt+MdIdt=0

⇒V=L1dIdt+L2dIdt−2MdIdt⇒V=L1dIdt+L2dIdt−2MdIdt

⇒V=(L1+L2−2M)dIdt⇒V=(L1+L2−2M)dIdt

The above equation is in the form of V=LEqdIdtV=LEqdIdt

Therefore, the equivalent inductance of series combination of inductors shown in the above figure is

LEq=L1+L2−2MLEq=L1+L2−2M

In this case, the equivalent inductance has been decreased by 2M. Hence, the above electrical circuit is an example of electrical coupling which is of opposing type.

Magnetic Coupling

Magnetic coupling occurs, when there is no physical connection between two coils (or inductors). This coupling can be of either aiding type or opposing type. It is based on whether the current enters at the dotted terminal or leaves from the dotted terminal.

Coupling of Aiding type

Consider the following electrical equivalent circuit of transformer. It is having two coils and these are called as primary and secondary coils.

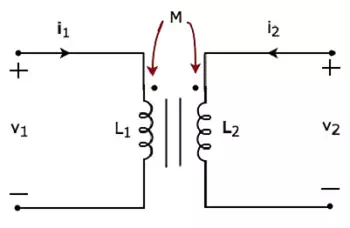
Description: Description: Magnetic Coupling Aiding

The currents flowing through primary and secondary coils are i₁ and i₂respectively. In this case, these currents enter at the dotted terminal of respective coil. Hence, the induced voltage in each coil will be having positive polarity at the dotted terminal due to the current flowing in another coil.

Apply KVL around primary coil.

$v_{1} - L_{1} \frac{d i_{1}}{d t} - M \frac{d i_{2}}{d t} = 0$

$\Rightarrow v_{1} = L_{1} \frac{d i_{1}}{d t} + M \frac{d i_{2}}{d t}$ v1=L1di1dt+Mdi2dtEquation 1

Apply KVL around secondary coil.

$v_{2} - L_{2} \frac{d i_{2}}{d t} - M \frac{d i_{1}}{d t} = 0$

$\Rightarrow v_{2} = L_{2} \frac{d i_{2}}{d t} + M \frac{d i_{1}}{d t}$ v2=L2di2dt+Mdi1dtEquation 2

In Equation 1 and Equation 2, the self-induced voltage and mutually induced voltage have the same polarity. Hence, the above transformer circuit is an example of magnetic coupling, which is of aiding type.

Coupling of Opposing Type

Consider the following electrical equivalent circuit of transformer.

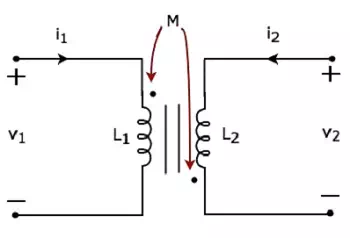
Description: Description: Magnetic Coupling Opposing

The currents flowing through primary and secondary coils are i₁ and i₂respectively. In this case, the current, i₁ enters at the dotted terminal of primary coil. Hence, it induces a voltage in secondary coil. So, positive polarity of the induced voltage is present at the dotted terminal of this secondary coil.

In the above circuit, the current, i₂ leaves from the dotted terminal of secondary coil. Hence, it induces a voltage in primary coil. So, negative polarity of the induced voltage is present at the dotted terminal of this primary coil.

Apply KVL around primary coil.

$v_{1} - L_{1} \frac{d i_{1}}{d t} + M \frac{d i_{2}}{d t} = 0$

$\Rightarrow v_{1} = L_{1} \frac{d i_{1}}{d t} - M \frac{d i_{2}}{d t}$ v1=L1di1dt−Mdi2dtEquation 3

Apply KVL around secondary coil.

$v_{2} - L_{2} \frac{d i_{2}}{d t} + M \frac{d i_{1}}{d t} = 0$

$\Rightarrow v_{2} = L_{2} \frac{d i_{2}}{d t} - M \frac{d i_{1}}{d t}$ v2=L2di2dt−Mdi1dtEquation 4

In Equation 3 and Equation 4, self-induced voltage and mutually induced voltage are having opposite polarity. Hence, the above transformer circuit is an example of magnetic coupling, which is of opposing type.