Ray Diagrams - Concave Mirrors

The theme of this unit has been that we see an object because light from the object travels to our eyes as we sight along a line at the object. Similarly, we see an image of an object because light from the object reflects off a mirror and travel to our eyes as we sight at the image location of the object. From these two basic premises, we have defined the image location as the location in space where light appears to diverge from. Ray diagrams have been a valuable tool for determining the path taken by light from the object to the mirror to our eyes. In this section of Lesson 3, we will investigate the method for drawing ray diagrams for objects placed at various locations in front of a concave mirror.

To draw these diagrams, we will have to recall the two rules of reflection for concave mirrors:

· Any incident ray traveling parallel to the principal axis on the way to the mirror will pass through the focal point upon reflection.

· Any incident ray passing through the focal point on the way to the mirror will travel parallel to the principal axis upon reflection.

Earlier in this lesson, the following diagram was shown to illustrate the path of light from an object to mirror to an eye.

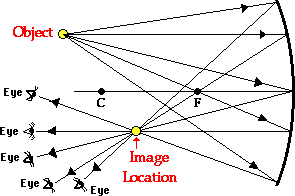
In this diagram five incident rays are drawn along with their corresponding reflected rays. Each ray intersects at the image location and then diverges to the eye of an observer. Every observer would observe the same image location and every light ray would follow the law of reflection. Yet only two of these rays would be needed to determine the image location since it only requires two rays to find the intersection point. Of the five incident rays drawn, two of them correspond to the incident rays described by our two rules of reflection for concave mirrors. Because they are the easiest and most predictable pair of rays to draw, these will be the two rays used through the remainder of this lesson

Step-by-Step Method for Drawing Ray Diagrams

The method for drawing ray diagrams for concave mirror is described below. The method is applied to the task of drawing a ray diagram for an object located beyond the center of curvature (C) of a concave mirror. Yet the same method works for drawing a ray diagram for any object location.

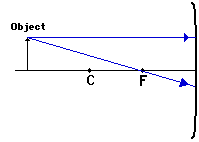1. Pick a point on the top of the object and draw two incident rays traveling towards the mirror.

Using a straight edge, accurately draw one ray so that it passes exactly through the focal point on the way to the mirror. Draw the second ray such that it travels exactly parallel to the principal axis. Place arrowheads upon the rays to indicate their direction of travel.

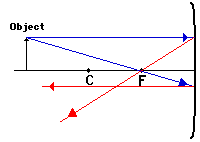2. Once these incident rays strike the mirror, reflect them according to the two rules of reflection for concave mirrors.

The ray that passes through the focal point on the way to the mirror will reflect and travel parallel to the principal axis. Use a straight edge to accurately draw its path. The ray that traveled parallel to the principal axis on the way to the mirror will reflect and travel through the focal point. Place arrowheads upon the rays to indicate their direction of travel. Extend the rays past their point of intersection.

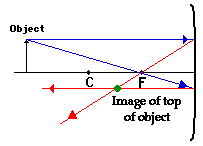3. Mark the image of the top of the object.

The image point of the top of the object is the point where the two reflected rays intersect. If your were to draw a third pair of incident and reflected rays, then the third reflected ray would also pass through this point. This is merely the point where all light from the top of the object would intersect upon reflecting off the mirror. Of course, the rest of the object has an image as well and it can be found by applying the same three steps to another chosen point. (See note below.)

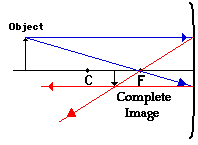4. Repeat the process for the bottom of the object.

The goal of a ray diagram is to determine the location, size, orientation, and type of image that is formed by the concave mirror. Typically, this requires determining where the image of the upper and lower extreme of the object is located and then tracing the entire image. After completing the first three steps, only the image location of the top extreme of the object has been found. Thus, the process must be repeated for the point on the bottom of the object. If the bottom of the object lies upon the principal axis (as it does in this example), then the image of this point will also lie upon the principal axis and be the same distance from the mirror as the image of the top of the object. At this point the entire image can be filled in.

Some students have difficulty understanding how the entire image of an object can be deduced once a single point on the image has been determined. If the object is a vertically aligned object (such as the arrow object used in the example below), then the process is easy. The image is merely a vertical line. In theory, it would be necessary to pick each point on the object and draw a separate ray diagram to determine the location of the image of that point. That would require a lot of ray diagrams as illustrated below.

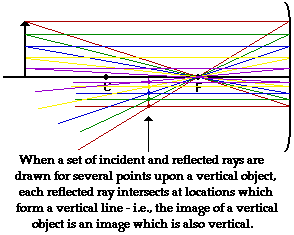
Fortunately, a shortcut exists. If the object is a vertical line, then the image is also a vertical line. For our purposes, we will only deal with the simpler situations in which the object is a vertical line that has its bottom located upon the principal axis. For such simplified situations, the image is a vertical line with the lower extremity located upon the principal axis.

The ray diagram above illustrates that when the object is located at a position beyond the center of curvature, the image is located at a position between the center of curvature and the focal point. Furthermore, the image is inverted, reduced in size (smaller than the object), and real. This is the type of information that we wish to obtain from a ray diagram. These characteristics of the image will be discussed in more detail in the next section of Lesson 3.

Once the method of drawing ray diagrams is practiced a couple of times, it becomes as natural as breathing. Each diagram yields specific information about the image. The two diagrams below show how to determine image location, size, orientation and type for situations in which the object is located at the center of curvature and when the object is located between the center of curvature and the focal point.

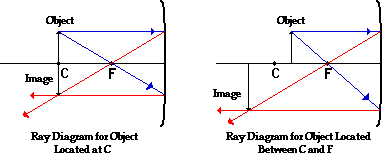
It should be noted that the process of constructing a ray diagram is the same regardless of where the object is located. While the result of the ray diagram (image location, size, orientation, and type) is different, the same two rays are always drawn. The two rules of reflection are applied in order to determine the location where all reflected rays appear to diverge from (which for real images, is also the location where the reflected rays intersect).

In the three cases described above - the case of the object being located beyond C, the case of the object being located at C, and the case of the object being located between C and F - light rays are converging to a point after reflecting off the mirror. In such cases, a real image is formed. As discussed previously, a real image is formed whenever reflected light passes through the image location. While plane mirrors always produce virtual images, concave mirrors are capable of producing both real and virtual images. As shown above, real images are produced when the object is located a distance greater than one focal length from the mirror. A virtual image is formed if the object is located less than one focal length from the concave mirror. To see why this is so, a ray diagram can be used.

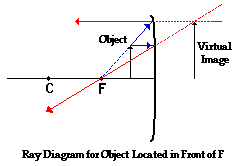A ray diagram for the case in which the object is located in front of the focal point is shown in the diagram at the right. Observe that in this case the light rays diverge after reflecting off the mirror. When light rays diverge after reflection, a virtual image is formed. As was done with plane mirrors, the image location can be found by tracing all reflected rays backwards until they intersect. For every observer, the reflected rays would seem to be diverging from this point. Thus, the point of intersection of the extended reflected rays is the image point. Since light does not actually pass through this point (light never travels behind the mirror), the image is referred to as a virtual image. Observe that when the object in located in front of the focal point, its image is an upright and enlarged image that is located on the other side of the mirror. In fact, one generalization that can be made about all virtual images produced by mirrors (both plane and curved) is that they are always upright and always located on the other side of the mirror.

Ray Diagram for an Object Located at the Focal Point

Thus far we have seen via ray diagrams that a real image is produced when an object is located more than one focal length from a concave mirror; and a virtual image is formed when an object is located less than one focal length from a concave mirror (i.e., in front of F). But what happens when the object is located at F? That is, what type of image is formed when the object is located exactly one focal length from a concave mirror? Of course a ray diagram is always one tool to help find the answer to such a question. However, when a ray diagram is used for this case, an immediate difficulty is encountered. The incident ray that begins from the top extremity of the object and passes through the focal point does not meet the mirror. Thus, a different incident ray must be used in order to determine the intersection point of all reflected rays. Any incident light ray would work as long as it meets up with the mirror. Recall that the only reason that we have used the two we have is that they can be conveniently and easily drawn. The diagram below shows two incident rays and their corresponding reflected rays.

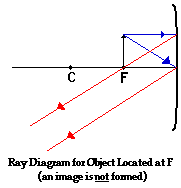
For the case of the object located at the focal point (F), the light rays neither converge nor diverge after reflecting off the mirror. As shown in the diagram above, the reflected rays are traveling parallel to each other. Subsequently, the light rays will not converge on the object's side of the mirror to form a real image; nor can they be extended backwards on the opposite side of the mirror to intersect to form a virtual image. So how should the results of the ray diagram be interpreted? The answer: there is no image!! Surprisingly, when the object is located at the focal point, there is no location in space at which an observer can sight from which all the reflected rays appear to be diverging. An image is not formed when the object is located at the focal point of a concave mirror.

Check Your Understanding

The diagram below shows two light rays emanating from the top of the object and incident towards the mirror. Describe how the reflected rays for these light rays can be drawn without actually using a protractor and the law of reflection.

See Answer

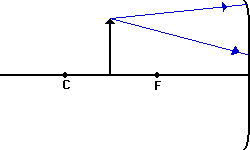
These two incident rays will pass through the image point for the top of the object. In fact, any light rays emanating from the top of the object will pass through the image point. Thus, merely construct a ray diagram to determine the image location; use the two rules of reflection. Then draw the reflected rays for the two given incident rays through the same image point.