Two Rules of Reflection for Concave Mirrors

Light always reflects according to the law of reflection, regardless of whether the reflection occurs off a flat surface or a curved surface. Using reflection laws allows one to determine the image location for an object. The image location is the location where all reflected light appears to diverge from. Thus to determine this location demands that one merely needs to know how light reflects off a mirror. In the previous section of Lesson 3, the image of an object for a concave mirror was determined by tracing the path of light as it emanated from an object and reflected off a concave mirror. The image was merely that location where all reflected rays intersected. The use of the law of reflection to determine a reflected ray is not an easy task. For each incident ray, a normal line at the point of incidence on a curved surface must be drawn and then the law of reflection must be applied. A simpler method of determining a reflected ray is needed.

The simpler method relies on two rules of reflection for concave mirrors. They are:

· Any incident ray traveling parallel to the principal axis on the way to the mirror will pass through the focal point upon reflection.

· Any incident ray passing through the focal point on the way to the mirror will travel parallel to the principal axis upon reflection.

These two rules of reflection are illustrated in the diagram below.

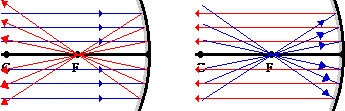
These two rules will greatly simplify the task of determining the image locations for objects placed in front of concave mirrors. In the next section of Lesson 3, these two rules will be applied to determine the location, orientation, size and type of image produced by a concave mirror. As the rules are applied in the construction of ray diagrams, do not forget the fact that the law of reflection holds for each of these rays. It just so happens that when the law of reflection is applied for a ray (either traveling parallel to the principal axis or passing through F) that strikes the mirror at a location near the principal axis, the ray will reflect in close approximation with the above two rules.