Other Multiple Mirror Systems
Besides right angle mirror systems, there is a wealth of
other multiple mirror systems that involve two or more mirrors. If two plane
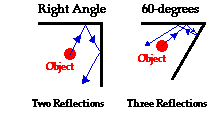
mirrors are placed together on one of their edges so as to form a right angle
mirror system and then the angle between them is decreased, some interesting
observations can be made. One observes that as the angle between the mirrors
decreases, the number of images that can be seen increases. In fact as the
angle between the mirrors approaches 0 degrees (i.e., the mirrors are parallel
to each other), the number of images approaches infinity.

 Determining
Image Locations for Multiple Mirror Systems
Determining
Image Locations for Multiple Mirror Systems
The generation of two images is not difficult to explain;
each of the two mirrors produces an image due to the single reflection of light
off one of the mirror faces to an observer's eye. The remaining images are
produced as the result of multiple reflections of light off more than one of
the faces. Right angle mirrors will allow a maximum of two reflections of light
from the object. But as the angle decreases, three, four, and even more
reflections can occur.
Determining the image locations for such multiple mirror
systems can become complicated. First determine the location of the primary
images using the principle that the image distance to the mirror is the same as the object distance to
the mirror. Each primary image forms a secondary image as
a result of a double reflection. By extending one of the mirror lines, a
primary image can be reflected (a geometry term, not a physics term)
across the second mirror line to form a secondary image - an image of an image. As an
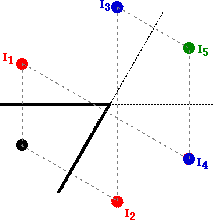
example, consider the diagram below for an object placed between two plane
mirrors that make a 60-degree angle. Images I1 and I2 are primary images formed by the two
plane mirrors. Image I3 was
found by reflecting image I2 across the extension of the top
mirror. And image I4 was
found by reflecting the image I1 across the side mirror. The process
can be repeated to determine the location of an image of an image of an image.
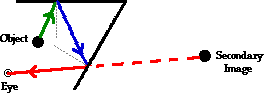
Ray diagrams for these multiple mirror systems are drawn much
like they were for right angle mirror systems. Once you have
located the images, begin by drawing a line of sight towards the image; this
would be the reflected ray that ultimately travels to your eye. For a secondary
image, this reflected ray is associated with an incident ray that had reflected
off the other face of the mirror. The law of reflection can be used to
determine the direction it was traveling as it was incident upon this face of
the mirror. Repeat this process to determine the point of reflections on each
face, tracing the path of light back to its origin - the object itself. A
completed ray diagram for a secondary image on a 60-degree mirror system is
shown below.
Flickr Physics Photo
With two plane mirrors oriented at a nearly 50
degree angle to one another, six different images are formed of an object.
A
Pair of Parallel Mirrors
When the two mirrors are aligned at a 0-degree angle with
each other (i.e., a parallel mirror system), there is an infinite number of
images. Each image is the result of an image
of an image, or an image
of an image of an image or an image of an image of ... .
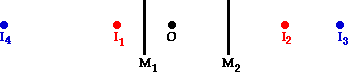
The diagram below shows the multiple images for a parallel mirror system.
Images I1 and I2 are primary images. Image I1 is the image resulting from the reflection of the object O across mirror M1 and image I2 is the image resulting from the reflection of the object O across mirror M2.
Image I3 is an image
of image I1, found by reflecting image I1 across mirror M2. Image I4 is an image of image I2;
found by reflecting image I2 across mirror M1. This
process could continue indefinitely, producing images of images for an infinite
number of images extending to the right of mirror M2 and to the left of mirror M1.
Multiple mirror systems are merely the extension of what we
have already learned about plane mirrors. The locating of images is an
extension of the principle that the image distance to the mirror is the same as the object distance to
the mirror. Drawing ray diagrams for multiple mirror
systems is an extension of the line of sight and law of reflection principles.
Flickr Physics Photo
This photo pictures a novelty item that
consists of a rectangular box with two mirrors on its top and bottom sides. The
top mirror is half-silvered allowing one to see through to objects behind it.
Several lights are embedded in the vertical wall of the box. The parallel
arrangement of the two mirrors creates multiple images which appear to be
stretching to "infinity".
Check Your Understanding
1. Rose Inhatt stands
between a set of parallel plane mirrors (M1 and M2) as shown in the
diagram below. There is a flower on Rose's hat that is located a distance of
0.4 m from M1 and a
distance of 1.0 m from M2. Since the mirrors are parallel, Rose will
see an infinite number of images of the flower as she looks in mirror M2.
These images stretch towards infinity. Some of the images are closer to the
mirror than others.
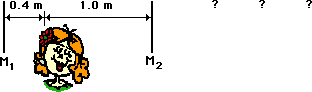
Determine the distance between mirror M2 and the...
a. ... nearest image ____________
b. ... second nearest image____________
c. ... the third nearest image ____________

1.0 m, 1.8 m, and 3.8 m
Rose will see a
primary image 1.0 m to the right of M2. She will see a secondary image 1.8 m to
the right of M2; this is the image of the image of the rose. Finally, there is
a tertiary image located 3.8 m to the right of M2. It is the image of the image
of an image. WOW!

