Image Formation in
Plane Mirrors
Why is an Image Formed?
In Lesson 1 of this unit of the Physics Classroom Tutorial,
the manner in which light reflected off objects in order to allow us to see
them was discussed. A major principle in that lesson was expressed as follows:
In
order to view an object, you must sight along a line at that object; and when
you do light will come from that object to your eye along the line of sight.
This very principle can be extended to the task of viewing
the image of an object in a plane (i.e., flat) mirror:
In
order to see the image of an object in a mirror, you must sight at the image;
when you sight at the image, light will come to your eye along that line of
sight.
The image location is thus located at that
position where observers are sighting when viewing the image of an object. It
is the location behind the mirror where all the light appears to diverge from.
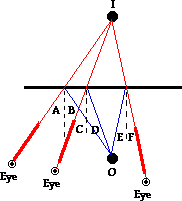
In the diagram below, three individuals are sighting at the image of an object
along three different lines of sight. Each person sees the image due to the
reflection of light off the mirror in accordance with the law of
reflection. When each line of sight is extended
backwards, each line will intersect at the same point. This point is the image
point of the object.
Locating
an Image via Parallax
This principle can be illustrated in a Physics class using a
5-foot plane mirror and a pair of large cylinders. One cylinder is placed in
front of the mirror and students from different locations in the room are asked
to sight at its image. The second cylinder is then aligned along the line of
sight and readjusted until it is in line with each person's line of sight.
Regardless of who is viewing the image and from where they are viewing the
image, each sight line must intersect in the same location. It is possible that
the second cylinder is aligned with one student's line of sight but not with
another student's. If this is so, then the cylinder is not placed at the exact
location of the image. This is depicted in the diagram below.
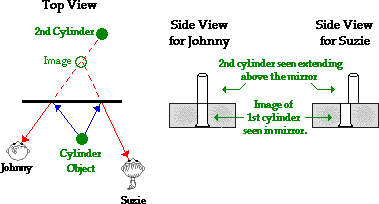
In a case such as this, the cylinder position is adjusted
until it is located at the position where all students in the classroom can see
it extending above the mirror and in line with the image that each student sees
when looking in the mirror. Only, then can we conclude the cylinder is located
at the image position.
Who
Can See an Image?
Since there is only one image for an object placed in front
of a plane mirror, it is reasonable that every sight line would intersect in a
single location. This location of intersection is known as the image location.
The image location is simply the one location in space where it
seems to every observer that the light is diverging from. Regardless of where
the observer is located, when the observer sights at the image location, the
observer is sighting along a line towards the same location that all other observers
are sighting. And as mentioned in an earlier lesson, the
perpendicular distance from this image location to the mirror is equal to the
perpendicular distance from the object location to the mirror. In fact, the
image location is directly across the mirror from the object location and an
equal distance from the mirror.
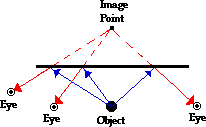
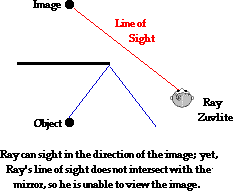
Of course, it is possible that certain individuals in the
room will be unable to view the image of an object in a plane mirror. Because
of the person's position relative to the image position and to the extremities
of the mirror, the person is unable to detect a ray of light reflecting to
their eye as they sight at the image location. This does not mean that there is
no image. Indeed, any object positioned in front of a plane mirror (or even to
the side of the plane mirror) has an image regardless of whether there are
people positioned in an appropriate location to view it. In the diagram below,
there is an image of an object located on the other side of the mirror.
However, Ray Zuvlite is unable to view the
image due to his position in the room. Ray is certainly able to sight in the
direction of the image location. However, the light from the object is unable
to reflect off the mirror in accordance with the law of reflection and travel to
his eye along his line of sight. Since light from the object does not make it
to his eye, Ray is unable to see the image of the object in the mirror.
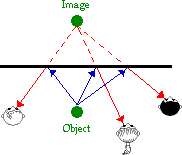
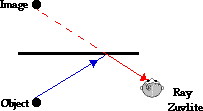
Of course, this problem could be remedied if the mirror were
wider, if the object were moved to the left or closer to the mirror, and/or if
Ray moved to the left. Repositioning the object, the mirror, and/or the person
could result in a ray of light from the object reflecting off the mirror and
traveling to Ray's eye. The diagram below depicts this remedy.
How
Does Reflection Lead to the Formation of Images?
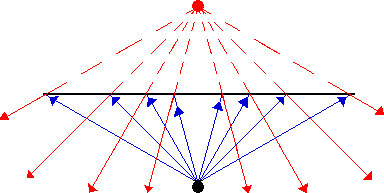
So why is an image formed by a plane mirror? An image is
formed because light emanates from an object in a variety of directions. Some
of this light (which we represent by rays) reaches the mirror and reflects off
the mirror according to the law of reflection. Each one of these rays of light
can be extended backwards behind the mirror where they will all intersect at a
point (the image point). Any person who is positioned along the line of one of
these reflected rays can sight along the line and view the image - a
representation of the object.
This principle of image formation is often applied in a
Physics lab. Suppose that a mirror is placed on a sheet of paper that is placed
on top of a piece of cardboard. A pin is positioned in an upright position (and
held in place by the cardboard) at a location in front of the mirror. A student
can sight along a line at the image of the pin from a variety of locations.
With one eye closed, a straightedge is used to assist in drawing the lines of
sight. These lines of sight are drawn from a variety of sighting locations.
Each line of sight can be extended backwards beyond the mirror. If the sight
lines are drawn correctly, then each line will intersect at the same location.
The location of intersection of all sight lines is the image location.
Validation of the accuracy of your sighting and ray tracing can be accomplished
by measuring angles of incidence and angles of reflection on the diagram. These
should be equal for each individual sight line. That is, angle A should equal
angle B; angle C should equal angle D; and angle E should equal angle F.
Finally, the object distance can be compared to the image distance; these
should also be equal.