Two Point Source Interference

Wave interference is a phenomenon that occurs when two waves meet while traveling along the same medium. The interference of waves causes the medium to take on a shape that results from the net effect of the two individual waves upon the particles of the medium. Wave interference can be constructive or destructive in nature. Constructive interference occurs at any location along the medium where the two interfering waves have a displacement in the same direction. For example, if at a given instant in time and location along the medium, the crest of one wave meets the crest of a second wave, they will interfere in such a manner as to produce a "super-crest." Similarly, the interference of a trough and a trough interfere constructively to produce a "super-trough." Destructive interference occurs at any location along the medium where the two interfering waves have a displacement in the opposite direction. For example, the interference of a crest with a trough is an example of destructive interference. Destructive interference has the tendency to decrease the resulting amount of displacement of the medium. Interference principles were first introduced in Unit 10 of The Physics Classroom Tutorial. The principles were subsequently applied to the interference of sound waves in Unit 11 of The Physics Classroom Tutorial.

A defining moment in the history of the debate concerning the nature of light occurred in the early years of the nineteenth century. Thomas Young showed that an interference pattern results when light from two sources meets up while traveling through the same medium. To understand Young's experiment, it is important to back up a few steps and discuss the interference of water waves that originate from two points.

In Unit 10, the value of a ripple tank in the study of water wave behavior was introduced and discussed. If an object bobs up and down in the water, a series water waves in the shape of concentric circles will be produced within the water. If two objects bob up and down with the same frequency at two different points, 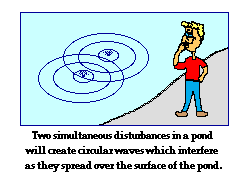then two sets of concentric circular waves will be produced on the surface of the water. These concentric waves will interfere with each other as they travel across the surface of the water. If you have ever simultaneously tossed two pebbles into a lake (or somehow simultaneously disturbed the lake in two locations), you undoubtedly noticed the interference of these waves. The crest of one wave will interfere constructively with the crest of the second wave to produce a large upward displacement. And the trough of one wave will interfere constructively with the trough of the second wave to produce a large downward displacement. And finally the crest of one wave will interfere destructively with the trough of the second wave to produce no displacement. In a ripple tank, this constructive and destructive interference can be easily controlled and observed. It represents a basic wave behavior that can be expected of any type of wave.

Two-Point Source Interference Patterns

The interference of two sets of periodic and concentric waves with the same frequency produces an interesting pattern in 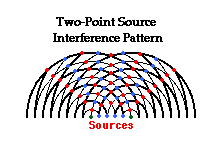a ripple tank. The diagram at the right depicts an interference pattern produced by two periodic disturbances. The crests are denoted by the thick lines and the troughs are denoted by the thin lines. Thus, constructive interference occurs wherever a thick line meets a thick line or a thin line meets a thin line; this type of interference results in the formation of an antinode. The antinodes are denoted by a red dot. Destructive interference occurs wherever a thick line meets a thin line; this type of interference results in the formation of a node. The nodes are denoted by a blue dot. The pattern is a standing wave pattern, characterized by the presence of nodes and antinodes that are "standing still" - i.e., always located at the same position on the medium. The antinodes (points where the waves always interfere constructively) seem to be located along lines - creatively called antinodal lines. The nodes also fall along lines - called nodal lines. The two-point source interference pattern is characterized by a pattern of alternating nodal and antinodal lines. There is a central line in the pattern - the line that bisects the line segment that is drawn between the two sources is an antinodal line. This central antinodal line is a line of points where the waves from each source always reinforce each other by means of constructive interference. The nodal andantinodal lines are included on the diagram below.

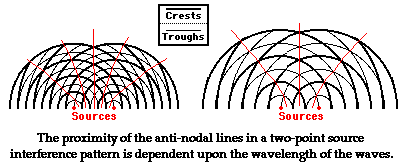
A two-point source interference pattern always has an alternating pattern of nodal and antinodal lines. There are however some features of the pattern that can be modified. First, a change in wavelength (or frequency) of the source will alter the number of lines in the pattern and alter the proximity or closeness of the lines. An increase in frequency will result in more lines per centimeter and a smaller distance between each consecutive line. And a decrease in frequency will result in fewer lines per centimeter and a greater distance between each consecutive line.

Second, a change in the distance between the two sources will also alter the number of lines and the proximity or closeness of the lines. When the sources are moved further apart, there are more lines produced per centimeter and the lines move closer together. These two general cause-effect relationships apply to any two-point source interference pattern, whether it is due to water waves, sound waves, or any other type of wave.

Two-Point Source Light Interference Patterns

Any type of wave, whether it be a water wave or a sound wave should produce a two-point source interference pattern if the two sources periodically disturb the medium at the same frequency. Such a pattern is always characterized by a pattern of alternating nodal andantinodal lines. Of course, the question should arise and indeed did arise in the early nineteenth century: Can light produce a two-point source interference pattern? If light is found to produce such a pattern, then it will provide more evidence in support of the wavelike nature of light.

Before we investigate the evidence in detail, let's discuss what one might observe if light were to undergo two-point source interference. What would happen if a "crest" of one light wave interfered with a "crest" of a second light wave? And what would happen if a "trough" of one light wave interfered with a "trough" of a second light wave? And finally, what would happen if a "crest" of one light wave interfered with a "trough" of a second light wave?

Whenever light constructively interferes (such as when a crest meeting a crest or a trough meeting a trough), the two waves act to reinforce one another and to produce a "super light wave." On the other hand, whenever light destructively interferes (such as when a crest meets a trough), the two waves act to destroy each other and produce no light wave. Thus, the two-point source interference pattern would still consist of an alternating pattern of antinodal lines and nodal lines. However for light waves, the antinodal lines are equivalent to bright lines and the nodal lines are equivalent to dark lines. If such an interference pattern could be created by two light sources and projected onto a screen, then there ought to be an alternating pattern of dark and bright bands on the screen. And since the central line in such a pattern is an antinodal line, the central band on the screen ought to be a bright band.

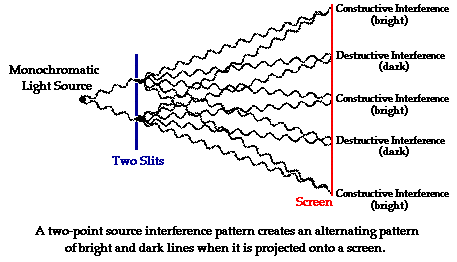
In 1801, Thomas Young successfully showed that light does produce a two-point source interference pattern. In order to produce such a pattern, monochromatic light must be used. Monochromatic light is light of a single color; by use of such light, the two sources will vibrate with the same frequency. It is also important that the two light waves be vibrating in phase with each other; that is, the crest of one wave must be produced at the same precise time as the crest of the second wave. (This is often referred to as coherent light.) To accomplish this, Thomas Young used a single light source and projected the light onto two pinholes. The light from the source will then diffract through the pinholes and the pattern can be projected onto a screen. Since there is only one source of light, the set of two waves that emanate from the pinholes will be in phase with each other. As expected, the use of a monochromatic light source and pinholes to generate in-phase light waves resulted in a pattern of alternating bright and dark bands on the screen. A typical appearance of the pattern is shown below.

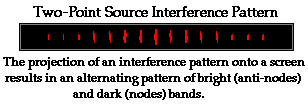
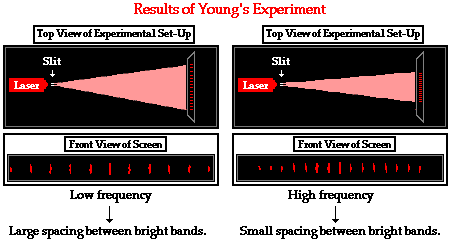
Young's two-point source interference experiment is often performed in a Physics course with laser light. It is found that the same principles that apply to water waves in a ripple tank also apply to light waves in the experiment. For instance, a higher frequency light source should produce an interference pattern with more lines per centimeter in the pattern and a smaller spacing between lines. Indeed this is observed to be the case. Furthermore, a greater distance between slits should produce an interference pattern with more lines percentimeter in the pattern and a smaller spacing between lines. Again, this is observed to be the case.

Most astounding of all is that Thomas Young was able to use wave principles to measure the wavelength of light. Details on the development of Young's equation and further information about his experiment are provided in Lesson 3 of this unit. For now, the emphasis is on how the same characteristics observed of water waves in a ripple tank are also observed of light waves. Thomas Young's findings provide even more evidence for the scientists of the day that light behaves as a wave. After all, can a stream of particles do all this?