Young's Experiment

The previous section of Lesson 3 discussed Thomas Young's effort to derive an equation relating the wavelength of a light source to reliably measured distances associated with a two-point source light interference pattern. The equation, known as Young's equation is:

λ = y • d / (m • L)

In 1801, Young devised and performed an experiment to measure the wavelength of light. As discussed in the previous part of this lesson, it was important that the two sources of light that form the pattern be coherent. The difficulty confronting Young was that the usual light sources of the day (candles, lanterns, etc.) could not serve as coherent light sources. Young's method involved using sunlight that entered the room through a pinhole in a window shutter. A mirror was used to direct the pinhole beam horizontally across the room. To obtain two sources of light, Young used a small paper card to break the single pinhole beam into two beams, with part of the beam passing by the left side of the card and part of the beam passing by the right side of the card. Since these two beams emerged from the same source - the sun - they could be considered coming from two coherent sources. Light waves from these two sources (the left side and the right side of the card) would interfere. The interference pattern was then projected onto a screen where measurements could be made to determine the wavelength of light.

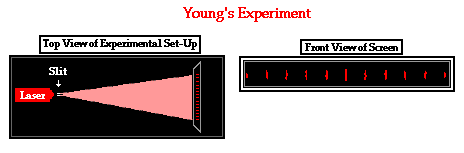
Today's classroom version of the same experiment is typically performed using a laser beam as the source. Rather than using a note card to split the single beam into two coherent beams, a carbon-coated glass slide with two closely spaced etched slits is used. The slide with its slits is most commonly purchased from a manufacturer who provides a measured value for the slit separation distance - the d value in Young's equation. Light from the laser beam diffracts through the slits and emerges as two separate coherent waves. The interference pattern is then projected onto a screen where reliable measurements can be made of L and y for a given bright spot with order value m. Knowing these four values allows a student to determine the value of the wavelength of the original light source.

To illustrate some typical results from this experiment and the subsequent analysis, consider the sample data provided below for d, y, L and m.

Data Table
Slit Separation (d)	0.250 mm
Distance from Slits to Screen (L)	9.78 m
Distance from AN0 to AN4(y)	10.2 cm
Order value (m)	4

(Note: AN₀ = central antinode and AN₄ = fourth antinode)

The determination of the wavelength demands that the above values for d, y, L and m be substituted into Young's equation.

λ = y • d / (m • L)

Careful inspection of the units of measurement is always advisable. The sample data here reveal that each measured quantity is recorded with a different unit. Before substituting these measured values into the above equation, it is important to give some thought to the treatment of units. One means of resolving the issue of nonuniform units is to simply pick a unit of length and to convert all quantities to that unit. If doing so, one might want to pick a unit that one of the data values already has so that there is one less conversion. A wise choice is to choose the meter as the unit to which all other measured values are converted. Since there are 1000 millimeters in 1 meter, the 0.250 mm is equivalent to 0.000250 meter. And since there are 100 centimeters in 1 meter, the 10.2 cm is equivalent to 0.102 m. Thus, the new values of d, y and L are:

d	0.000250 m
L	9.78 m
y	0.102 m
m	4

While the conversion of all the data to the same unit is not the only means of treating such measured values, it might be the most advisable - particularly for those students who are less at ease with such conversions.

Now that the issue regarding the units of measurement has been resolved, substitution of the measured values into Young's equation can be performed.

λ = (0.102 m) • (0.000250 m) / [ (4) • (9.78 m) ]

λ = 6.52 x 10^-7 m

As is evident here, the wavelength of visible light is rather small. For this reason wavelength is often expressed using the unit nanometer, where 1 meter is equivalent to 10⁹ nanometers. Multiplying by 10⁹will convert the wavelength from meters to nanometers (abbreviated nm).

λ = 652 nm

Check Your Understanding

1. The diagram below depicts the results of Young's Experiment. The appropriate measurements are listed on the diagram. Use these measurements to determine the wavelength of light in nanometers. (GIVEN: 1 meter = 10⁹ nanometers)

See Answer

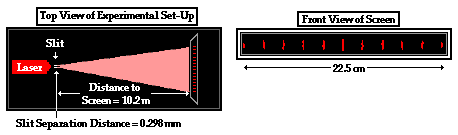
Answer: 657 nm

First, identify known values in terms of their corresponding variable symbol:

L = 10.2 m = 1020 cm	y = 22.5 cm
m = 10	d = 0.298 mm = 0.0298 cm

(Note: m was chosen as 10 since the y distance corresponds to the distance from the 5th bright band on one side of the central band and the 5th bright band on the other side of the central band.)

Then convert all known values to an identical unit. In this case, cm has been chosen as the unit to use. The converted values are listed in the table above.

Substitute all values into Young's equation and perform calculation of the wavelength. The unit of wavelength is cm.

λ = y • d / ( m • L)

λ = ( 22.5 cm ) • ( 0.0298 cm ) / [ ( 10 ) • ( 1020 cm ) ]

λ = 6.57 x 10^-5 cm

Finally convert to nanometers using a conversion factor. If there are 10⁹ nm in 1 meter, then there must be 10⁷ nm in the smaller centimeter.

λ = ( 6.57 x 10^-5 cm ) • ( 10⁷ nm / 1 cm ) = 657 nm

2. A student uses a laser and a double-slit apparatus to project a two-point source light interference pattern onto a whiteboard located 5.87 meters away. The distance measured between the central bright band and the fourth bright band is 8.21 cm. The slits are separated by a distance of 0.150 mm. What would be the measured wavelength of light?

See Answer

Answer: 524 nm

First, identify known values in terms of their corresponding variable symbol:

L = 5.87 m = 587 cm	y = 8.21 cm
m = 4	d = 0.150 mm = 0.0150 cm

Then convert all known values to an identical unit. In this case, cm has been chosen as the unit to use. The converted values are listed in the table above.

Substitute all values into Young's equation and perform calculation of the wavelength. The unit of wavelength is cm.

λ = y • d / ( m • L)
λ = ( 8.21 cm ) • ( 0.0150 cm ) / [ ( 4 ) • ( 587 cm ) ]
λ = 5.24 x 10^-5 cm

Finally convert to nanometers using a conversion factor. If there are 10⁹ nm in 1 meter, then there must be 10⁷ nm in the smaller centimeter.

λ = ( 5.24 x 10^-5 cm ) • ( 10⁷ nm / 1 cm ) = 524 nm

3. The analysis of any two-point source interference pattern and a successful determination of wavelength demands an ability to sort through the measured information and equating the values with the symbols in Young's equation. Apply your understanding by interpreting the following statements and identifying the values of y, d, m and L. Finally, perform some conversions of the given information such that all information share the same unit.

a. Two slits separated by 0.250 mm produces an interference pattern in which the fifth dark band is located 12.8 cm from the central antinode when the screen is placed a distance of 8.2 meters away.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit.

y = 12.8 cm	d = 0.250 mm	m = 4.5	L = 8.2 meters
Converted values:
y = 12.8 cm	d = 0.0250 cm	m = 4.5	L = 820 cm

(Note that m = 4.5 represents the fifth nodal position or dark band from the central bright band. Also note that the given values have been converted to cm.)

b. An interference pattern is produced when light is incident upon two slits that are 50.0 micrometers apart. The perpendicular distance from the midpoint between the slits to the screen is 7.65 m. The distance between the two third-order antinodes on opposite sides of the pattern is 32.9 cm.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

y = 32.9 cm	d = 50.0 µm	m = 6	L = 7.65 m
Converted values:
y = 32.9 cm	d = 0.00500 cm	m = 6	L = 765 cm

(Note that m = 6 corresponds to six spacings. There are three spacings between the central antinode and the third antinode. The stated distance is twice as far so the m value must be doubled. Also note that the given values have been converted to cm. There are 10⁶ µm in one meter; so there are 10⁴ µm in one centimeter.)

c. The fourth nodal line on an interference pattern is 8.4 cm from the first antinodal line when the screen is placed 235 cm from the slits. The slits are separated by 0.25 mm.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit.

y = 8.4 cm	d = 0.25 mm	m = 2.5	L = 235 cm
Converted values:
y = 8.4 cm	d = 0.025 cm	m = 2.5	L = 235 cm

( Note that the fourth nodal line is assigned the order value of 3.5. Also note that the given values have been converted to cm.)

d. Two sources separated by 0.500 mm produce an interference pattern 525 cm away. The fifth and the second antinodal line on the same side of the pattern are separated by 98 mm.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit.

y = 98 mm	d = 0.500 mm	m = 3	L = 525 cm
Converted values:
y = 9.8 cm	d = 0.0500 cm	m = 3	L = 525 cm

( Note that there are three spacings between the second and the fifth bright bands. Since all spacings are the same distance apart, the distance between the second and the fifth bright bands would be the same as the distance between the central and the third bright bands. Thus, m = 3. Also note that the given values have been converted to cm.)

e. Two slits that are 0.200 mm apart produce an interference pattern on a screen such that the central maximum and the 10th bright band are distanced by an amount equal to one-tenth the distance from the slits to the screen.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

y = 0.1 • L	d = 0.200 mm	m = 10	L - not stated
Converted values:
y = 0.1 • L	d = 0.200 mm	m = 10	L - not stated

( Note that there are 10 spacings between the central anti-node and the tenth bright band or tenth anti-node. And observe that they do not state the actual values of L and y; the value of y is expressed in terms of L. )

f. The fifth antinodal line and the second nodal line on the opposite side of an interference pattern are separated by a distance of 32.1 cm when the slits are 6.5 m from the screen. The slits are separated by 25.0 micrometers.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

y = 32.1 cm	d = 25.0 µm	m = 6.5	L = 6.5 m
Converted values:
y = 32.1 cm	d = 0.00250 cm	m = 6.5	L = 650 cm

( Note that there are five spacings between the central anti-node and the fifth anti-node. And there are 1.5 spacings from the central anti-node in the opposite direction out to the second nodal line. Thus, m = 6.5. Also note that the given values have been converted to cm. There are 10⁶ µm in one meter; so there are 10⁴ µm in one centimeter.)

g. If two slits 0.100 mm apart are separated from a screen by a distance of 300 mm, then the first-order minimum will be 1 cm from the central maximum.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

y = 1 cm	d = 0.100 mm	m = 0.5	L = 300 mm
Converted values:
y = 1 cm	d = 0.0100 cm	m = 0.5	L = 30.0 cm

( Note that a the first-order minimum is a point of minimum brightness or a nodal position. The first-order minimum is the first nodal position and is thus the m = 0.5 node. Also note that the given values have been converted to cm. )

h. Consecutive bright bands on an interference pattern are 3.5 cm apart when the slide containing the slits is 10.0 m from the screen. The slit separation distance is 0.050 mm.

y =

d =

m =

L =

See Answer

This question simply asks to equate the stated information with the variables of Young's equation and to perform conversions such that all information is in the same unit. 

y = 3.5 cm	d = 0.050 mm	m = 1	L = 10.0 m
Converted values:
y = 3.5 cm	d = 0.0050 cm	m = 1	L = 1000 cm

( Note that the spacing between adjacent bands is given. This distance is equivalent with the distance from the central bright band to the first antinode. Thus, m = 1. Also note that the given values have been converted to cm. )