Young's Equation
Previously
in Lesson 3 we have seen how circular waves from two sources can
interfere in the surrounding space to produce a pattern of antinodes and nodes.
The nodal positions are present at locations where destructive interference
always occurs and the path difference is a half-number of wavelengths.
The antinodal positions
are present at locations where constructive interference always occurs and the
path difference is equivalent to a whole number of wavelengths.
|
Antinodal Points: |
PD = m • λ |
where m = 0, 1, 2, 3, 4, ... |
|
|
|
|
|
Nodal Points: |
PD = m • λ |
where m = 0.5, 1.5, 2.5, 3.5,
... |
The discussion of
the interference patterns was introduced by referring to the interference of
water waves in a ripple tank. All waves behave the same,
whether they are water waves created by vibrating sources in a ripple tank,
sound waves produced by two speakers, or light waves produced by two light
sources. For water waves in a ripple tank, the resulting pattern would include
locations along the water's surface where water was vibrating up and down with
unusually large amplitudes (antinodes). And there would be other locations
where the water was relatively undisturbed (nodes). For sound waves produced by
two speakers, the interference pattern would be characterized by locations
where the sound intensity was large due to constructive interference
(antinodes). And there would be other locations where sound cancellation occurs
and the sound intensity was relatively faint or not even heard at all (nodes).
But what would be observed in a two-point source light interference pattern?
A
Light Interference Pattern
As in any
two-point source interference pattern, light waves from two coherent,
monochromatic sources (more on coherent and monochromatic later) will interfere constructively and destructively to produce a pattern
of antinodes and nodes. Light traveling through the air is typically not seen
since there is nothing of substantial size in the air to reflect the light to
our eyes. Thus, the pattern formed by light interference cannot be seen unless
it is somehow projected onto some form of a screen or a sheet of paper. When
light from the two sources is projected onto a screen, the pattern becomes
quite evident. Locations where light constructively interferes corresponds to
an abnormally bright spot. Locations where light destructively interferes
corresponds to an abnormally dark spot. That is, the antinodes are locations
where light from the two individual sources are reinforcing each other and
correspond to points of brightness or maximum intensity (sometimes referred to
as maxima). And the nodes are locations where light from
the two individual sources are destroying each other and correspond to points
of darkness or minimum intensity (sometimes referred to as minima).
Red laser light
passing through two narrowly spaced slits is typically used in the classroom to
produce this effect. Thus, a pattern of bright red and dark fringes or bands is
observed on a screen as shown in the diagram below.
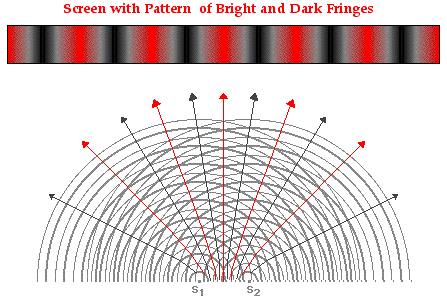
In the above
pattern, the central bright band where light displays maximum intensity
corresponds to a point on the central antinodal line.
The bright bands to the right and the left of the central bright band
correspond to the projection of other antinodal lines
onto the screen. The dark bands correspond to the projection of the nodal lines
onto the screen.
As mentioned earlier in Lesson 3, each antinodal and nodal line is
assigned a number or order value (m). The red band of maximum brightness
located in the center of screen (the
central maximum) is assigned an order number of m = 0. The other bright red
bands to the left and the right of the central maximum are assigned whole number
values of 1, 2, 3, ... as shown in the
diagram below. The dark bands on the pattern are assigned half number values of
0.5, 1.5, 2.5, ... as shown in the diagram
below.
The goal of such
a classroom demonstration is typically twofold: 1) to demonstrate the wavelike
nature of light by displaying its ability to interfere; and 2) to use the
interference pattern to measure the wavelength of light and verify the
mathematical model of two-point source interference.
Derivation
of Young's Equation
In 1801, this
experiment was performed for the first time by Thomas Young. Young expanded the
mathematical model presented above by relating the wavelength of light to observable and measurable
distances. Today, an experimental setup similar to that of Thomas Young's is
commonly used in a Physics classroom to repeat the experiment and to measure
the wavelength of light. In the experiment as it is commonly performed today,
light from a laser beam is passed through two narrowly spaced slits in a slide
or sheet of paper. The light diffracts through the slits and interferes in the
space beyond the slits. Thus, the slits serve as the two sources. The
interference pattern is then projected onto a screen, paper or a whiteboard
located several meters away. The spatial separation of nodes and antinodes on
the screen is clearly seen.
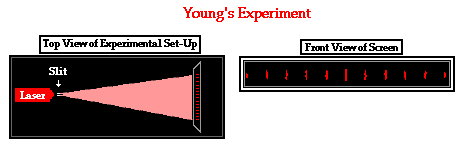
The most reliably
measured distances in this experimental procedure are the distance from the
sources to the screen, the distance between the sources, and the distance
between the bright spots that appear on the screen. Thus, Thomas Young derived
an equation that related the wavelength of the light to these measurable
distances. The derivation, which involves relatively simple geometry,
right-angle trigonometry and algebra, is repeated below.
The diagram below
on the left depicts two sources labeled S1 and S2 and separated by some distance d. Point P is a point on the screen that happens to be located on some
nodal or antinodal line; as such, there is
an order value (m) associated with
this point. Point C is the central point on the screen. The distance from point
P to point C as measured perpendicular to the central antinodal line
will be referred to as y. The screen is located a distance of L from the
sources. In the following derivation, the wavelength of light will be related
to the quantities d, m, y and L.
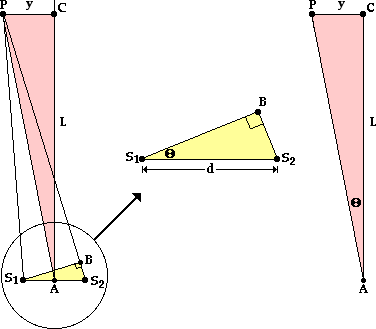
On the diagram
above, source S2 is
further from point P than source S1 is. The extra distance traveled by waves from S2 can be determined if a line is drawn
from S1 perpendicular
to the line segment S2P. This line is drawn in the diagram on the
left above; it intersects line segment S2P at point B. If point P (a
bright spot on the screen) is located a great distance from the sources, then
it follows that the line segment S1P is the same distance as BP. As
such, the line segment S2B is simply the path difference. That is,
the small distance S2B is equal to the difference in distance traveled by the two waves from their individual
sources to point P on the screen. The logic is as follows:
|
|
Assertion |
Logic/Rationale |
|
i |
S2P = S2B + BP |
See diagram above left |
|
ii |
|
If screen is very far away (L
>>> y), then lines S1P and BP are || |
|
iii |
S1P = BP |
If S1P and BP are || and
line S1B is perpendicular to BP, then the length BP = length S1P |
|
iv |
S2P = S2B + S1P |
Since S1P = BP, the
expression S1P can be substituted into i |
|
v |
S2B = S2P - S1P |
Algebraic manipulation of iv; subtract
S1P from each side |
|
vi |
S2B is the PD |
The path difference (PD) is defined as
| S2P - S1P | |
Note that step ii
in the logical proof above demanded that an assumption be made: the screen must
be very far away compared to the spacing between point P and the central antinodal line. That is, L >>> y. This is an
assumption that underlies Young's derivation of his wavelength equation. The
equation is only as valid as this assumption is true.
The yellow
triangle in the diagram on the left above is enlarged and redrawn in the middle
of the graphic. The triangle is a right triangle with an angle theta and a
hypotenuse of d. Using the sine function, it can be stated that
sine(Θ) = S2B / d
But since it has
been previously stated that the path difference (PD) is equal to the length of
the line segment S2B, the above
equation can be rewritten as
sine(Θ) = PD / d
It can be further
asserted that the pink triangle (∆ S1BS2) and
the yellow triangle (∆ ACP) in the diagrams above are similar
triangles. To prove that any two triangles are similar, one must show that they
have two corresponding angles that are equal. Since the line segment PC was
drawn perpendicular to the central antinodal line,
it forms a 90-degree angle with the line AC. Thus, the corresponding angles S1BS2 and ACP are equal.
The second set of
corresponding angles of equal measure is 
S1S2B and APC. This can be proven by returning
to the assumption that the screen is very far away (L >>> y). Clearly,
the lines S1S2 and
PC are parallel lines. As such, the diagonal line S2P creates two
alternating angles that are equal in measure - that is, S2PC = S1S2B.
Since it is assumed that L >>> y, the line segment S2P and
AP are roughly parallel to each other and thus make roughly the same angle with
the line segment S1S2. With this assumption, it is thus
proven that APC = S2PC. Since the S2PC is equal to both S1S2B and APC, it follows that S1S2B = APC. As such, the
pink triangle (∆S1BS2) and the yellow triangle
(∆ACP) have two corresponding angles that are equal and thus are similar
triangles.
If the pink
triangle (∆S1BS2) and the yellow triangle
(∆ACP) are similar, all corresponding angles are equal in measure, and so S2S1B
= PAC. These two
angles are labeled as theta in the diagrams
above. The use of trigonometric functions allows one to relate the angle theta
to the reliably measured distances d, y and L.
|
sine Θ = PD / d |
|
tangent Θ = y / L |
The above logic
has consistently assumed that the screen upon which the interference pattern is
projected is very far away; that is, L >>> y. This is typically the
case for visible light interference patterns. In fact, the L value is typically
on the order of several meters while the y value is on the order of a couple
of centimeters. For such dimensions, the angle
theta is less than 1 degree. For such small angles, the approximation that the
sine 
= tangent can be made. Taking 1 degree as a
sample angle, calculated values of the sine and tangent can be compared.
|
sine (1 deg)
= 0.017452406 |
|
tangent (1 deg)
= 0.017455064 |
Note that the
values for the sine and the tangent of 1 degree show agreement out to the
fourth significant digit. Since the sine and the tangent of these small angles
are approximately equal, we can state that their ratio of lengths (as stated
above) is also equal. That is,
PD / d = y / L
In the previous
section of Lesson 3, it was shown that the path difference (PD) for any point
on the pattern is equal to m • λ, where m is the order number of that
point and λ is the wavelength. By substitution,
m • λ / d = y / L
As a final step
in the derivation, the equation can be algebraically manipulated so that the
wavelength (λ) is by itself:
λ = y • d / (m • L)
As set forth by
the derivation above, the wavelength of laser light can be experimentally determined
by selecting a point (referred to as point P) on a nodal and antinodal line of known order value (m) and making the
following measurements:
· the
distance between the slits or sources of the two light waves (d)
· the
perpendicular distance from the point P to a point on the central antinodal line (y)
· the
distance from point P to the sources (L)
The Importance of Coherent Light Sources
Visible light
waves - those that humans can see - have an abnormally short wavelength. For
instance, red light has a wavelength of about 650 nanometers.
Since there are one billion nanometers in a
meter, and one thousand millimeters in a
meter, the wavelength of red light is less than one-thousandth of a millimeter. That's a very short wave. And being a short
wave, the distance between positions of constructive interference and positions
of destructive interference is very small. Thus, the effects of interference
for visible light waves are difficult to observe.
Complicating the
task of observing the interference of visible light waves is the fact that
light from the two sources must be coherent. Two light sources that maintain a constant
phase difference with each other are said to be coherent light sources. Light
visible to the human eye makes a complete cycle of vibration from crest to trough and back to crest
in roughly 10-15 seconds.
If we think of a light wave as a transverse wave pattern with crests and
troughs, then a crest is typically created every 10-15 seconds. Consider two light sources
producing light waves at the same frequency, but one source is creating a crest
just prior to the moment in time when the other source is creating a crest.
Such light sources are not at the same phase in their cycle of light
production. They are said to be out of phase. Yet if they maintain the same
difference in phase, they are considered coherent light sources. Even if the
sources of light do not stay in
step with each other, as long
as the amount by which they are out of step remains the same over time, the
light sources are said to be coherent.
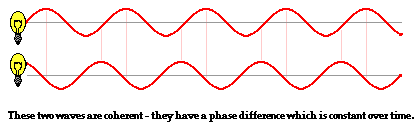
Typical light
sources such as incandescent light bulbs have an intrinsic irregularity
associated with the manner in which they produce light. The production of light
results when atoms of the filaments or source become electrically excited and
produce an electromagnetic or light wave. Since these excitations occur in an
unpredictably random fashion, the light waves that they produce do not maintain
a constant phase difference with each other. Approximately once every 10-8 seconds, a source will randomly alter
its phase. While waves from these sources will interfere to produce an
interference pattern, the lack of coherence means that the pattern will
constantly change with time. In fact, the patterns change so rapidly with time
(once every 10-8 seconds)
that there is no possibility that the human eye could ever discern a pattern.
To produce a stable and unchanging interference pattern, it is essential that
the two sources be coherent.
In this section,
the logic and mathematics associated with Young's equation was presented. we will investigate how Thomas Young was able to
conduct an experiment with two coherent sources of light in order to make a
reliable measurement of the wavelength of light.
Check Your Understanding
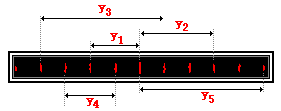1. When determining the wavelength of light, measurements must be made
of y, d, m and L. The y value is dependent upon the chosen dark or bright spot
and thus the m value. Consider the projected pattern of bright and dark spots
on a screen as shown below. For each y measurement, identify the corresponding mvalue. Then see if you can observe a generality about the relationship
between the spacing between adjacent bright spots and the y and m value.
|
Selected Measurement |
m value |
|
y1 = 6.4 cm |
____________ |
|
y2 = 9.6 cm |
____________ |
|
y3 = 16.0 cm |
____________ |
|
y4 = 6.4 cm |
____________ |
|
y5 = 16.0 cm |
____________ |
Note that the y / m ratio in the table below is a constant ratio
for all five measurements. This ratio represents the spacing between adjacent
bright spots on the screen. Since this ratio is a constant ratio, one could
conclude that the distance across the screen between any two bright spots -
whether adjacent or non-adjacent and whether to the central bright spot or any
bright spot - can be measured and used in Young's equation as long as it
corresponds to an m value which represents the number of spacings. In this context, a spacing is
referred to as a spacing between adjacent bright spots.
|
Selected Measurement |
m value |
y / m Ratio |
|
y1 = 6.4
cm |
2 |
3.2 cm |
|
y2 = 9.6
cm |
3 |
3.2 cm |
|
y3 = 16.0
cm |
5 |
3.2 cm |
|
y4 = 6.4
cm |
2 |
3.2 cm |
|
y5 = 16.0
cm |
5 |
3.2 cm |
2. Young's
equation describes the mathematical relationship between wavelength and
measurable quantities in a two-point source interference experiment.
λ = y • d / (m • L)
Describe the
effect of alterations in d, L and λ upon the spacing between bright spots
in a two-point source interference pattern; complete the following statements.
a. Altering the distance between sources (d) by a
factor of 2 would cause the y value to ____________ (increase or decrease) by a
factor of _____.
b. Altering the
distance between sources (d) by a factor of 0.5 (one-half) would cause the y value to ____________
(increase or decrease) by a factor of _____.
c. Altering the distance between the sources and
the screen (L) by a factor of
3 would cause the y value to ____________ (increase or decrease) by a factor of
_____.
d. Altering the
distance between the sources and the screen (L) by a factor of 0.25 (one-fourth) would cause the y value to
____________ (increase or decrease) by a factor of _____.
e. Altering the
wavelength of light (λ) by a factor of
1.5 (three-halves) would cause the y value to ____________ (increase or
decrease) by a factor of _____.
This question targets the effect of alterations in d, L and
λ upon the spacing between bright spots (y). Thus, the first place to
begin involves re-arranging Young's equation so that y is by itself on one side
of the equation:
y = m • L • λ / d
Now observe that y is directly proportional to the L and λ values and inversely
proportional to the d value.
a. Altering the distance
between sources (d)
by a factor of 2 would cause the y value to decrease by a factor of 2. That is, the y value will
be one-half its original value.
b. Altering the distance between sources (d) by a factor of 0.5
(one-half) would cause the y value to increase by a factor of 2. That is, the y value will be two times its original value.
c. Altering the distance
between the sources and the screen (L)
by a factor of 3 would cause the y value to increase by a factor of 3. That is, the y value will
be three times its original value.
d. Altering the distance between the sources and the screen (L) by a factor of 0.25
(one-fourth) would cause the y value to decrease by a factor of 4. That is, the y value will be one-fourth its original value.
e. Altering the
wavelength of light (λ) by a factor of 1.5 (three-halves) would cause the y value
to increase by a factor of 1.5. That is, the y value will
be three-halves its original value.