The Path Difference
Two-point source interference occurs when waves from one
source meet up with waves from another source. If the source of waves produces
circular waves, then the circular wavefronts will meet within the medium to produce a
pattern. The pattern is characterized by a collection of nodes and antinodes
that lie along nearly straight lines referred to as antinodal lines
and nodal lines. If the wave sources have identical frequencies, then there
will be an antinodal line in the exact center of the pattern and an alternating series
of nodal and antinodallines to the left and the right of the central antinodal line.
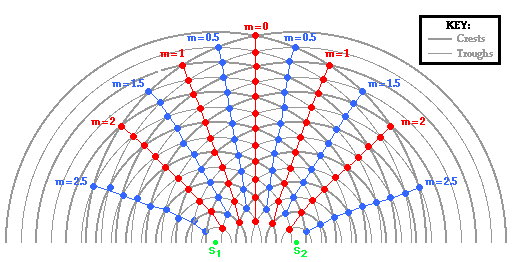
As discussed in the previous section of Lesson 3, each line in
the pattern is assigned a name (e.g., first antinodal line) and an order number (represented by
the symbol m). A representative two-point source interference pattern with
accompanying order numbers (m values) is shown below.
In this part of Lesson 3, we will investigate the rationale
behind the numbering system and develop some mathematical equations that relate
the features of the pattern to the wavelength of the waves. This investigation
will involve the analysis of several antinodal and nodal locations on a typical
two-point source interference pattern. It will be assumed in the discussion
that the wave sources are producing waves with identical frequencies (and
therefore identical wavelengths).
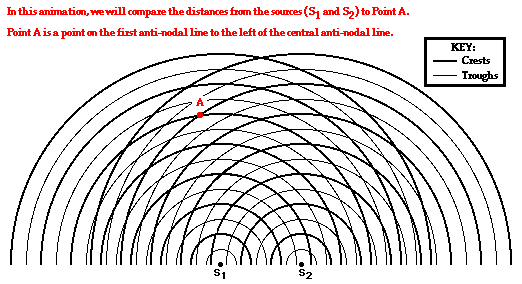
To begin, consider the pattern shown in the animation below.
Point A is a point located on the first antinodal line. This specific antinode is formed as
the result of the interference of a crest from Source 1 (S1) meeting
up with a crest from Source 2 (S2). The two wave crests are taking
two different paths to the same location to constructively interfere to form
the antinodal point.
The crest traveling from Source 1 (S1) travels a
distance equivalent to 5 full waves; that is, point A is a distance of 5
wavelengths from Source 1 (S1). The crest traveling from Source 2 (S2)
travels a distance equivalent to 6 full waves; point A is a distance of 6
wavelengths from Source 2 (S2). While the two wave crests are
traveling a different distance from their sources, they meet at point A in such
a way that a crest meets a crest. For this specific location on the pattern,
the difference in distance traveled (known as the path difference and
abbreviated as PD) is
PD = | S1A - S2A | = | 5λ -
6λ | = 1λ
(Note the path difference or PD is the difference in
distance traveled by the two waves from their respective sources to a given point on
the pattern.)
For point A on the first antinodal line (m =1), the path difference is
equivalent to 1 wavelength. But will all points on the first antinodal line
have a path difference equivalent to 1 wavelength? And if all points on the
first antinodal line have a path difference of 1 wavelength, then will all points
on the second antinodal line have a path difference of 2 wavelengths? And what about the
third antinodal line? And what about the nodal lines? These questions are
investigated in the diagrams below through the analysis of the path difference for
other points located on antinodal and nodal lines.
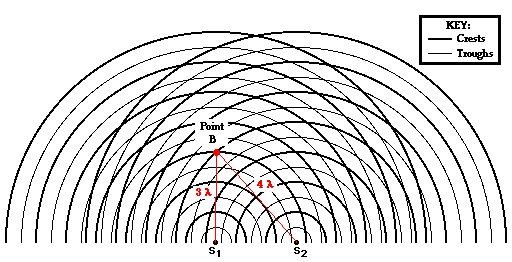
Point B in the diagram below is also located on the
first antinodal line. The point is formed as a wave crest travels a distance of 3
wavelengths from point S1 and
meets with a second wave crest that travels a distance 4 wavelengths from S2.
The difference in distance traveled by the two waves from their sources to
point B is
PD = | S1B - S2B | = | 3λ -
4λ | = 1λ
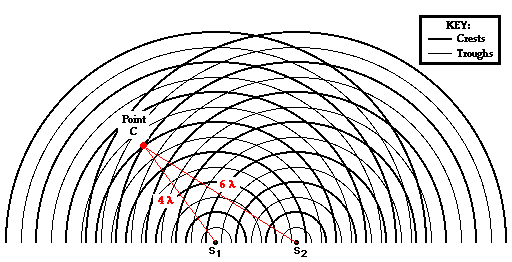
Now we will analyze Point C, which is located on the
second antinodal line (see the diagram below). The point is formed as a wave crest
travels a distance of 4 wavelengths from point S1 and meets with a second wave crest
that travels a distance 6 wavelengths from S2. The difference in
distance traveled by the two waves from their sources to point C is
PD = | S1C - S2C | = |
4 λ - 6 λ | = 2 λ
The analysis continues for this same pattern as we explore
the path difference for locations on nodal lines. Point D is located on the
first nodal line (see the diagram below). The point is formed as a wave crest
travels a distance of 5 wavelengths from point S1 and meets with a wave trough that
travels a distance 4.5 wavelengths from S2. The difference in
distance traveled by the two waves from their sources to point D is
PD = | S1D - S2D | = |
5 λ - 4.5 λ | = 0.5 λ
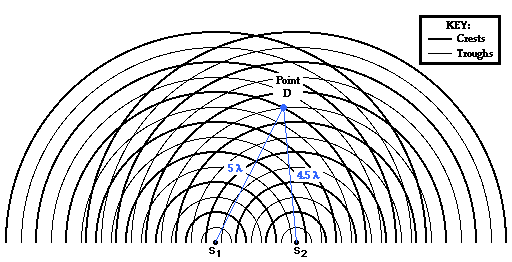
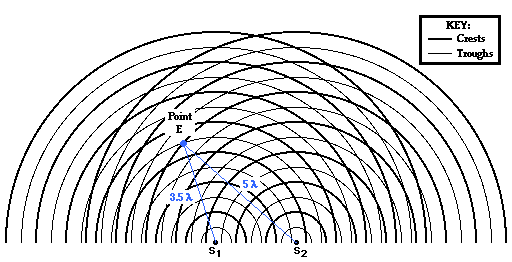
Point E in the diagram below is located on the second nodal
line. The point is formed as a wave trough travels a distance of 3.5
wavelengths from point S1 and
meets with a wave crest that travels a distance 5 wavelengths from S2.
The difference in distance traveled by the two waves from their sources to
point E is
PD = | S1E - S2E | = |
3.5 λ - 5 λ | = 1.5 λ
The information in the above analyses is summarized in the
table below. Other points on other antinodal and nodal lines are marked on the diagram
below and their distance from the sources and their path difference are also
summarized in the same table. Inspect the table and see if you can find a
pattern evident in the numbers.
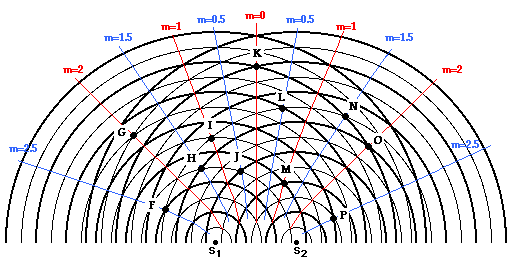
Summary of the Path Difference
Analysis
|
Point |
Antinode |
Order # |
Distance |
Distance |
Path |
|
A |
Antinode |
1 |
5 λ |
6 λ |
1 λ |
|
B |
Antinode |
1 |
3 λ |
4 λ |
1 λ |
|
C |
Antinode |
2 |
4 λ |
6 λ |
2 λ |
|
D |
Node |
0.5 |
5 λ |
4.5 λ |
0.5 λ |
|
E |
Node |
1.5 |
3.5 λ |
5 λ |
1.5 λ |
|
F |
Node |
2.5 |
2 λ |
4.5 λ |
2.5 λ |
|
G |
Antinode |
2 |
4.5 λ |
6.5 λ |
2 λ |
|
H |
Node |
1.5 |
2.5 λ |
4 λ |
1.5 λ |
|
I |
Antinode |
1 |
3.5 λ |
4.5 λ |
1 λ |
|
J |
Node |
0.5 |
2.5 λ |
3 λ |
0.5 λ |
|
K |
Antinode |
0 |
6 λ |
6 λ |
0 λ |
|
L |
Node |
0.5 |
5 λ |
4.5 λ |
0.5 λ |
|
M |
Antinode |
1 |
3 λ |
2 λ |
1 λ |
|
N |
Node |
1.5 |
6 λ |
4.5 λ |
1.5 λ |
|
O |
Antinode |
2 |
6 λ |
4 λ |
2 λ |
|
P |
Node |
2.5 |
4 λ |
1.5 λ |
2.5 λ |
What pattern do you see in the numerical values for path
difference above? An inspection of the path difference column and the order
number column reveals that there is a clear relationship between these two
quantities. The path difference is always the order number multiplied by the
wavelength. That is,
PD = m • λ
Furthermore, one might notice that the path difference is a
whole number of wavelengths for the antinodal positions and a half number of
wavelengths for the nodal positions. That is,
|
Antinodal Points: |
PD = m • λ |
where m = 0, 1, 2, 3, 4, ... |
|
|
|
|
|
Nodal Points: |
PD = m • λ |
where m = 0.5, 1.5, 2.5, 3.5,
... |
Explaining
the Path Difference Equation
A tedious inspection of a variety of antinodal and
nodal points on a typical pattern reveals the above relationships. But why? Why
would constructive interference occur when the difference in distance traveled by
two waves is equivalent to a whole number of wavelengths? And why would
destructive interference occur when the difference in distance traveled by
two waves is equivalent to a half number of wavelengths? To answer these
questions, consider the diagrams below.
The diagram below shows two waves traveling along different
paths from different sources to the same point in such a way that a crest is
meeting a crest. Constructive interference will occur at this point. The wave
from Source 1 (S1) travels a distance of 6 wavelengths (you can
trace your finger over the wave to help you count wavelengths). The wave from
Source 2 (S2) travels a distance of 7 wavelengths to reach the same
point. The difference in distance traveled by the two waves is one full wavelength.
That is, the path difference is 1 λ. When the path difference is one
full wavelength, a crest meets a crest and constructive interference occurs.
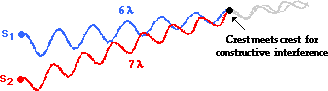
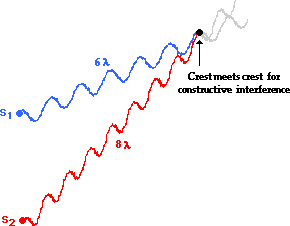
How does a path difference of two wavelengths cause
constructive interference? The diagram below shows this. Two waves traveling
along different paths from different sources meet at the same point in such a
way that a crest is meeting a crest; constructive interference occurs. The wave
from Source 1 (S1) travels a distance of 6 wavelengths. The wave
from Source 2 (S2) travels a distance of 8 wavelengths to reach the
same point. The difference in distance traveled by the two waves is two full wavelengths;
that is, the path difference is 2 λ. When the path difference is two
full wavelengths, a crest meets a crest and constructive interference occurs.
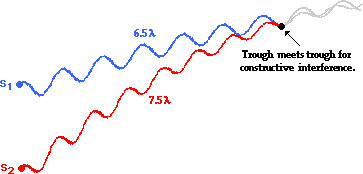
The previous two examples involve the meeting of a crest with
a crest. Under what conditions will a trough meet a trough? The diagram below
depicts this. Once more, the two waves travel different paths from their
different sources and meet in such a manner to constructively interfere; only
this time the constructive interference results from a trough meeting a trough.
Observe that the wave from Source 1 (S1) travels a distance of 6.5
wavelengths. The wave from Source 2 (S2) travels a distance of 7.5
wavelengths to reach the same point. The difference in distance traveled by
the two waves is one full wavelength; that is, the path difference is
1 λ.
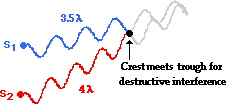
The above examples pertain to the constructive interference
that occurs for locations on antinodal lines. In each case, a path difference of
a whole number of wavelengths causes a crest to meet a crest or a trough to
meet a trough. But what about destructive interference? The diagram below
depicts the destructive interference of two waves from the sources. Observe
that the wave from Source 1 (S1) travels a distance of 3.5
wavelengths. The wave from Source 2 (S2) travels a distance of 4
wavelengths to reach the same point. The difference in distancetraveled by
the two waves is one-half a wavelength; that is, the path difference is
0.5 λ. Whenever the two waves have
a path difference of one-half a wavelength, a crest from one source will meet a
trough from the other source. Destructive interference occurs for path
differences of one-half a wavelength.
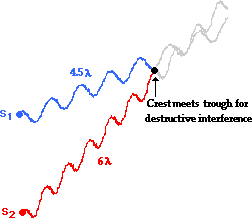
An additional example of destructive interference is shown
below. Observe that the wave from Source 1 (S1) travels a distance
of 4.5 wavelengths. The wave from Source 2 (S2) travels a distance
of 6 wavelengths to reach the same point. The difference in distance traveled by
the two waves is three-halves a wavelength; that is, the path difference
is 1.5  . Whenever the
two waves have a path difference of 1.5 wavelengths, a crest from one source
will meet a trough from the other source and destructive interference will
occur.
. Whenever the
two waves have a path difference of 1.5 wavelengths, a crest from one source
will meet a trough from the other source and destructive interference will
occur.
In summary, the analysis of the two-point source interference
patterns reveals the following equations:
|
Antinodal Points: |
PD = m • λ |
where m = 0, 1, 2, 3, 4, ... |
|
|
|
|
|
Nodal Points: |
PD = m • λ |
where m = 0.5, 1.5, 2.5, 3.5,
... |
A simple wave model demonstrates why these relationships
exist.
In the next part of Lesson 3 we will investigate the nature of a two-point
source light interference and make the connection between these simple ripple
tank patterns and the observations made by Thomas Young when he first
demonstrated two-point source light interference in the early 1800s.
Check Your Understanding
1. Two point sources, 3.0 cm apart, are generating periodic
waves in phase. A point on the third antinodal line of the wave pattern is 10 cm from
one source and 8.0 cm from the other source. Construct a sketch of the physical
situation and determine the wavelength of the waves. PSYW

Answer: 0.667 cm
The
distances from the sources to the antinode are known: S1P = 8 cm and
S2P = 10 cm. And since the antinode lies on the third antinodal line, m = 3. The distances between the
sources is known , but will be of little
importance. Using PD = m • λ, we can solve for wavelength.
PD = | S1P
- S2P | = | 8 cm - 10 cm | = 2 cm.
So
by substitution,
λ = PD / m
= (2 cm) / 3 = 0.667 cm
2. Two point sources are generating periodic waves in phase.
The wavelength is 4.0 cm. A point on the second antinodal line is 30.0 cm from the nearest source.
How far is this point from the farthest source? Begin by constructing a sketch
of the physical situation. PSYW

Answer: 38 cm
"Point P" is on the second antinodal line,
so m = 2. The wavelength (λ) is 4.0 cm. From the equation PD = m • λ,
the path difference (PD) can be found.
PD = 2 • 4.0 cm
= 8.0 cm
So point P is 8
cm further from the farther source than it is from the nearer source. So if P
is 30.0 cm from the nearest souce, then it is 38
cm from the furthest source.
3. Two point sources are generating periodic waves in phase.
The wavelength of the waves is 3.0 cm. A point on a nodal line is 25 cm from
one source and 20.5 cm from the other source. Construct a sketch of the
physical situation and determine the nodal line number. PSYW

Answer: m = 1.5 (second nodal line)
The distance from "point P" to the near source is 20.5
cm, S1P = 20.5 cm. And the distance from "point P" to the
further source is 25 cm; S2P = 25 cm. The path difference is found as
PD = | S1P
- S2P | = | 20.5 cm - 25 cm | = 4.5 cm.
The wavelength (λ) is 3 cm. Using PD = m • λ, we can
solve for the nodal line number.
m = PD / λ
= (4.5 cm) / 3 = 1.5
The point P is
on the second nodal line.
4. Two point sources are generating periodic waves in phase.
A point on the fourth nodal line is 25.0 cm from one source and 39.0 cm from
the farthest source. Construct a sketch of the physical situation and determine
the wavelength. PSYW

Answer: 4.0 cm
The
distance from "point P" to the near source is 25.0 cm (S1P
= 25.0 cm). And the distance from "point P" to the further source is
39.0 cm (S2P = 39.0 cm). The path difference is found as
PD = | S1P
- S2P | = | 25.0 cm - 39.0 cm | = 14.0 cm.
Since
the point is on the fourth nodal line, m = 3.5. Using PD = m • λ, we can
solve for the wavelength (λ).
λ = PD / m =
(14.0 cm) / 3.5 = 4.0 cm