Mathematics of Two-Point Source Interference
Anatomy of a Two-Point Source Interference Pattern
This unit of The Physics Classroom Tutorial focused on the
nature of light as a wave. Evidence that led scientists to believe that light
had a wavelike nature was presented. One piece of evidence centered around the ability of one light wave to interfere with
another light wave. This interference is most obvious if
monochromatic light from two coherent sources is allowed to interfere. In
Lesson 3 of this unit, we will focus upon the mathematical nature of two-point
source light interference. The relationship between the wavelength of light and
the specific features of a two-point source interference pattern will be
described. The means by which Thomas Young used this relationship to measure
the wavelength of light will be discussed.
In Lesson 1, the nature of
the interference pattern produced by two bobbing sources in a ripple tank
(water tank) was discussed.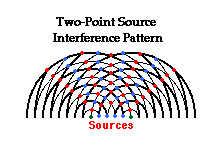 
The diagram at the right depicts the pattern resulting from the
propagation of water waves across the surface of the water. The waves propagate
outward from the point sources, forming a series of concentric circles about
the source. In the diagram, the thick lines represent wave crests and the thin
lines represent wave troughs. The crests and troughs from the two sources
interfere with each other at a regular rate to produce nodes (pictured in blue
on the diagram) and antinodes (pictured in red) along the water surface. The
nodal positions are locations where the water is undisturbed; the antinodalpositions
are locations where the water is undergoing maximum disturbances above and
below the surrounding water level. One unique feature of the two-point source interference
pattern is that the antinodal and nodal positions all lie along distinct lines. Each line can be
described as a relatively straight hyperbola. The spatial separation between
the antinodal and nodal lines in the pattern is related to the wavelength of the
waves. The mathematical relationship will be explored later in this lesson. For
now, we will investigate the underlying causes of this unique pattern and
introduce some nomenclature (naming conventions) that will be utilized
throughout the lesson.
The animation below shows a series of concentric circles
about two point sources (labeled as S1 and S2). The pattern could be the
result of water waves in a ripple tank resulting from two vibrating sources; or
the result of sound waves from two speakers traveling through a room; or the
result of two light waves moving through a room after passing through two slits
or pinholes in a sheet of paper. Like the diagram above, the thick lines
represent wave crests and the thin lines represent wave troughs. The red dots
in the animation represent theantinodal positions; the blue dots represent the nodal positions. The red
lines drawn through the antinodal points (red dots) are referred to as antinodal lines
and the blue lines drawn through the nodal points (blue dots) are referred to
as nodal lines.
A naming and numbering system is used to refer to these antinodal and
nodal lines. An antinodal line extends outward from the sources in the exact center of
the pattern. This antinodal line is referred to as the central antinodal line. More antinodal lines are present to the left and to the
right of the central antinodal line. These are referred to as the first antinodal line, the second antinodal line, the third antinodal line (if present), etc. Each antinodal line is separated by a nodal line. The
nodal lines are also named; the first nodal line to the left or to the right of
the central antinodal line is referred to as the first nodal
line. The second nodal line and the third nodal
line are found as one moves further to the left and to the right of the center of
the pattern.
Each line in the pattern is assigned a number, known as the order number and
represented by the letter m. The numbering
system associated with this pattern is just as creative as the naming system.
The central antinodal line is assigned an order number of 0. The firstantinodal line
is assigned an order number of 1; the second antinodal line is assigned an order number of 2;
the third antinodal line is assigned an order number of 3; etc. Nodal lines are
assigned half-numbers. The first nodal line, located between the central antinodal line
(m = 0) and the first antinodal line (m = 1) is assigned the order number of 0.5. The second nodal
line, located between the first antinodal line (m = 1) and the second antinodal line
(m = 2) is assigned the order number of 1.5. Finally, the third nodal line,
located between the secondantinodal line (m = 2) and the third antinodal line (m = 3) is assigned the order number
of 2.5. Subsequently, if one were to start in the center of
the pattern and observe the lines (both antinodal and nodal) and associated numbers to the
left or to the right of the centralantinodal line, the numbers would start at 0 and
increase by one-half:
0 
0.5 1 1.5 2 2.5 etc.
Each whole number is associated with an antinodal line
and each half-number is associated with a nodal line. (The numbering and naming
systems used here for nodal lines differs slightly from that used in many
textbooks. The reason for the numbering system will be more
clear after the next part of this lesson.)
Check Your Understanding
1. Observe the two-point source interference pattern shown
below. Several points are marked and labeled with a letter.
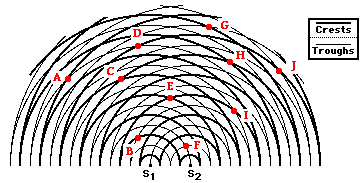
Which of the labeled points are ...
a.
... on nodal lines?
b. ... on antinodal lines?
c. ... formed as the result of constructive interference?
d. ... formed as the result of destructive interference?
a. Nodal Lines: A, B, D, G
(Look for the
interference of crests with troughs; that is, thick and thin lines.)
b. Antinodal Lines: C, E, F, H, I, J
(Look for the
interference of crests with crests or troughs with troughs; that is, thick and
thick lines or thin and thin lines.)
2. Observe the two-point source interference pattern shown
below. Several points are marked and labeled with a letter.
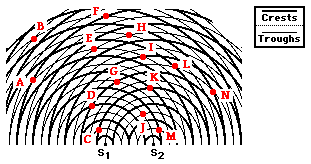
Which of the labeled points are ...
a.
... on the central antinodal line?
b. ... on the first antinodal line?
c. ... on the second antinodal line?
d. ... on the first nodal line?
e. ... on the second nodal line?
f. ... on the third nodal line?
a. Central Antinodal Line (m
= 0): H
b. First Antinodal Line (m =
1): E, J, K
c. Second Antinodal Line (m
= 2): B, D
d. First Nodal Line (m = 0.5): F, G, I
e. Second Nodal Line (m = 1.5): L
f. Third Nodal
Line (m = 2.5): A, C, M, N