Behavior of Sound Waves
Interference
and Beats
Wave interference is the
phenomenon that occurs when two waves meet while traveling along the same
medium. The interference of waves causes the medium to take on a shape that
results from the net effect of the two individual waves upon the particles of
the medium. As mentioned in a previous unit of The Physics Classroom Tutorial, if two
upward displaced pulses having the same shape meet up with one another while
traveling in opposite directions along a medium, the medium will take on the
shape of an upward displaced pulse with twice the amplitude of the two
interfering pulses. This type of interference is known as constructive
interference. If an upward displaced pulse and a downward
displaced pulse having the same shape meet up with one another while traveling
in opposite directions along a medium, the two pulses will cancel each other's
effect upon the displacement of the medium and the medium will assume the
equilibrium position. This type of interference is known as destructive
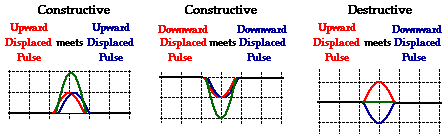
interference. The diagrams below show two waves - one is
blue and the other is red - interfering in such a way to produce a resultant
shape in a medium; the resultant is shown in green. In two cases (on the left
and in the middle), constructive interference occurs and in the third case (on
the far right, destructive interference occurs.
But how can sound waves that do not possess upward and
downward displacements interfere constructively and destructively? Sound is a
pressure wave that consists of compressions and rarefactions. As a compression passes through a section of
a medium, it tends to pull particles together into a small region of space,
thus creating a high-pressure region. And as a rarefaction passes through a
section of a medium, it tends to push particles apart, thus creating a
low-pressure region. The interference of sound waves causes the particles of
the medium to behave in a manner that reflects the net effect of the two
individual waves upon the particles. For example, if a compression (high
pressure) of one wave meets up with a compression (high pressure) of a second
wave at the same location in the medium, then the net effect is that that
particular location will experience an even greater pressure. This is a form of
constructive interference. If two rarefactions (two low-pressure disturbances)
from two different sound waves meet up at the same location, then the net
effect is that that particular location will experience an even lower pressure.
This is also an example of constructive interference. Now if a particular
location along the medium repeatedly experiences the interference of two
compressions followed up by the interference of two rarefactions, then the two
sound waves will continually reinforce each other and produce a very loud
sound. The loudness of the sound is the result of the particles at that
location of the medium undergoing oscillations from very high to very low
pressures. As mentioned in a previous unit, locations along the medium where constructive
interference continually occurs are known as anti-nodes. The animation below shows two sound waves
interfering constructively in order to produce very large oscillations in
pressure at a variety of anti-nodal locations. Note that compressions are labeled with a C and rarefactions are labeled with an R.

Now if two sound waves interfere at a given location in such
a way that the compression of one wave meets up with the rarefaction of a
second wave, destructive interference results. The net effect of a compression
(which pushes particles together) and a rarefaction (which pulls particles
apart) upon the particles in a given region of the medium is to not even cause
a displacement of the particles. The tendency of the compression to push
particles together is canceled by the
tendency of the rarefactions to pull particles apart; the particles would
remain at their rest position as though there wasn't even a disturbance passing
through them. This is a form of destructive interference. Now if a particular
location along the medium repeatedly experiences the interference of a
compression and rarefaction followed up by the interference of a rarefaction
and a compression, then the two sound waves will continually cancel each other and no sound is heard. The
absence of sound is the result of the particles remaining at rest and behaving
as though there were no disturbance passing through it. Amazingly, in a
situation such as this, two sound waves would combine to produce no sound. As
mentioned in a previous unit, locations along the medium where destructive
interference continually occurs are known as nodes.
Two
Source Sound Interference
A popular Physics demonstration involves the interference of
two sound waves from two speakers. The speakers are set approximately 1-meter
apart and produced identical tones. The two sound waves traveled through the air in front of the speakers,
spreading out through the room in spherical fashion. A snapshot in time of the
appearance of these waves is shown in the diagram below. In the diagram, the
compressions of a wavefront are represented
by a thick line and the rarefactions are represented by thin lines. These two
waves interfere in such a manner as to produce locations of some loud sounds
and other locations of no sound. Of course the loud sounds are heard at
locations where compressions meet compressions or rarefactions meet
rarefactions and the "no sound" locations appear wherever the
compressions of one of the waves meet the rarefactions of the other wave. If
you were to plug one ear and turn the other ear towards the place of the
speakers and then slowly walk across the room parallel to the plane of the
speakers, then you would encounter an amazing phenomenon. You would
alternatively hear loud sounds as you approached anti-nodal locations and
virtually no sound as you approached nodal locations. (As would commonly be
observed, the nodal locations are not true nodal locations due to reflections
of sound waves off the walls. These reflections tend to fill the entire room
with reflected sound. Even though the sound waves that reach the nodal
locations directly from the speakers destructively interfere, other waves
reflecting off the walls tend to reach that same location to produce a pressure
disturbance.)

Destructive interference of sound waves becomes
an important issue in the design of concert halls and auditoriums. The rooms
must be designed in such as way as to
reduce the amount of destructive interference. Interference can occur as the
result of sound from two speakers meeting at the same location as well as the
result of sound from a speaker meeting with sound reflected off the walls and
ceilings. If the sound arrives at a given location such that compressions meet
rarefactions, then destructive interference will occur resulting in a reduction
in the loudness of the sound at that location. One means of reducing the
severity of destructive interference is by the design of walls, ceilings, and
baffles that serve to absorb sound rather than reflect it. This will be
discussed in more detail later in Lesson 3.
The destructive interference of sound waves can also be used
advantageously in noise reduction systems. Earphones have
been produced that can be used by factory and construction workers to reduce
the noise levels on their jobs. Such earphones capture sound from the environment
and use computer technology to produce a second sound wave that one-half cycle out of phase. The combination
of these two sound waves within the headset will result in destructive
interference and thus reduce a worker's exposure to loud noise.
Musical Beats and Intervals
Interference of sound waves has widespread applications in
the world of music. Music seldom consists of sound waves of a single frequency
played continuously. Few music enthusiasts would be impressed by an orchestra
that played music consisting of the note with a pure tone played by all
instruments in the orchestra. Hearing a sound wave of 256 Hz (middle C) would become
rather monotonous (both literally and figuratively). Rather, instruments are
known to produce overtones when played resulting in a sound that consists of a
multiple of frequencies. Such instruments are described as being rich in
tone color. And even the best choirs will earn their money when two singers sing two notes (i.e.,
produce two sound waves) that are an octave apart. Music is a mixture of sound waves that typically
have whole number ratios between the frequencies associated with their notes.
In fact, the major distinction between music and noise is that noise consists
of a mixture of frequencies whose mathematical relationship to one another is
not readily discernible. On the other hand, music consists of a mixture of
frequencies that have a clear mathematical relationship between them. While it may be true that
"one person's music is another person's noise" (e.g., your music
might be thought of by your parents as being noise), a physical analysis of
musical sounds reveals a mixture of sound waves that are mathematically related.
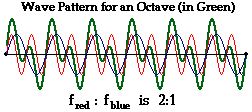
To demonstrate this nature of music, let's consider one of
the simplest mixtures of two different sound waves - two sound waves with a 2:1
frequency ratio. This combination of waves is known as an octave. A simple
sinusoidal plot of the wave pattern for two such waves is shown below. Note
that the red wave has two times the frequency of the blue wave. Also observe
that the interference of these two waves produces a resultant (in green) that
has a periodic and repeating pattern. One might say that two sound waves that
have a clear whole number ratio between their frequencies interfere to produce
a wave with a regular and repeating pattern. The result is music.
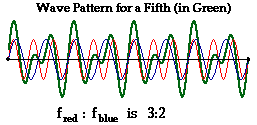
Another simple example of two sound waves with a clear
mathematical relationship between frequencies is shown below. Note that the red
wave has three-halves the frequency of the blue wave. In the music world, such
waves are said to be a fifth apart and represent a popular musical interval.
Observe once more that the interference of these two waves produces a resultant
(in green) that has a periodic and repeating pattern. It should be said again:
two sound waves that have a clear whole number ratio between their frequencies
interfere to produce a wave with a regular and repeating pattern; the result is
music.
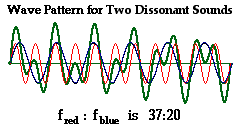
Finally, the
diagram below illustrates the wave pattern produced by two dissonant or
displeasing sounds. The diagram shows two waves interfering, but this time
there is no simple mathematical relationship between
their frequencies (in computer terms, one has a wavelength of 37 and the other
has a wavelength 20 pixels). Observe (look carefully) that the pattern of the
resultant is neither periodic nor repeating (at least not in the short sample
of time that is shown). The message is clear: if two sound waves that have no
simple mathematical relationship between their frequencies interfere to produce
a wave, the result will be an irregular and non-repeating pattern. This tends
to be displeasing to the ear.
A final
application of physics to the world of music pertains to the topic of beats. Beats are the
periodic and repeating fluctuations heard in the intensity of a sound when two
sound waves of very similar frequencies interfere with one another. The diagram
below illustrates the wave interference pattern resulting from two waves (drawn
in red and blue) with very similar frequencies. A beat pattern is characterized
by a wave whose amplitude is changing at a regular rate. Observe that the beat
pattern (drawn in green) repeatedly oscillates from zero amplitude to a large
amplitude, back to zero amplitude throughout the pattern. Points of
constructive interference (C.I.) and destructive interference (D.I.) are labeled on the diagram. When constructive interference
occurs between two crests or two troughs, a loud sound is heard. This
corresponds to a peak on the beat pattern (drawn in green). When destructive
interference between a crest and a trough occurs, no sound is heard; this
corresponds to a point of no displacement on the beat pattern. Since there is a
clear relationship between the amplitude and the loudness, this beat pattern
would be consistent with a wave that varies in volume at a regular rate.
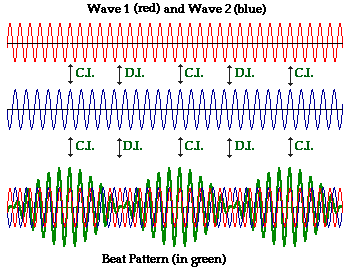
Beat Frequency
The beat frequency refers to the rate at which the volume is heard
to be oscillating from high to low volume. For example, if two complete cycles
of high and low volumes are heard every second, the beat frequency is 2 Hz. The
beat frequency is always equal to the difference in frequency of the two notes
that interfere to produce the beats. So if two sound waves with frequencies of
256 Hz and 254 Hz are played simultaneously, a beat frequency of 2 Hz will be
detected. A common physics demonstration involves producing beats using two
tuning forks with very similar frequencies. If a tine on one of two identical
tuning forks is wrapped with a rubber band, then that tuning forks frequency
will be lowered. If both tuning forks are vibrated together, then they produce
sounds with slightly different frequencies. These sounds will interfere to
produce detectable beats. The human ear is capable of detecting beats with
frequencies of 7 Hz and below.
A piano tuner frequently utilizes the
phenomenon of beats to tune a piano string. She will pluck the string and tap a
tuning fork at the same time. If the two sound sources - the piano string and
the tuning fork - produce detectable beats then their frequencies are not
identical. She will then adjust the tension of the piano string and repeat the
process until the beats can no longer be heard. As the piano string becomes
more in tune with the tuning fork, the beat frequency will be reduced and
approach 0 Hz. When beats are no longer heard, the piano string is tuned to the
tuning fork; that is, they play the same frequency. The process allows a piano
tuner to match the strings' frequency to the frequency of a standardized set of
tuning forks.
Important Note: Many of
the diagrams on this page represent a sound wave by a sine wave. Such a wave
more closely resembles a transverse wave and may mislead people into thinking
that sound is a transverse wave. Sound is not a transverse wave, but rather a longitudinal wave. Nonetheless, the variations in pressure with time take on
the pattern of a sine wave and thus a sine wave is often used to represent the
pressure-time features of a sound wave.
Check Your Understanding
Two speakers are arranged so that sound waves with the same
frequency are produced and radiate through the room. An interference pattern is
created (as represented in the diagram at the right). The thick lines in the
diagram represent wave crests and the thin lines represent wave troughs. Use
the diagram to answer the next two questions.
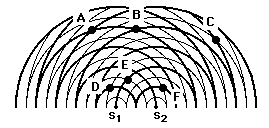 1. At which of the labeled point(s)
would constructive interference occur?
1. At which of the labeled point(s)
would constructive interference occur?
a. B only
b. A, B, and C
c. D, E, and F
d. A and B

Answer: D
Both points A
and B are on locations where a crest meets a crest.
2. How many of the six labeled points
represent anti-nodes?
|
a. 1 |
b. 2 |
c. 3 |
d. 4 |
e. 6 |

Answer: B
Only points A
and B are antinodes; the other points are points where crests and troughs meet.
3. A tuning fork with a frequency of 440 Hz is played simultaneously with a fork with a
frequency of 437 Hz. How many beats will be heard over a period of 10 seconds?

Answer: 30 beats
The beat
frequency will be 3 Hz; thus in 10 seconds, there should be 30 beats.
4. Why don't we hear beats when different keys on the piano
are played at the same time?

Our ears can
only detect beats if the two interfering sound waves have a difference in
frequency of 7 Hz or less. No two keys on the piano are that similar in
frequency.