Closed-End Air Columns
In the previous part of Lesson 5, the formation of a standing wave patterns in an open-end instrument
was discussed. The mathematics of the harmonic frequencies associated with such
standing wave patterns were developed. This part of Lesson 5 will use similar
principles to develop the standing wave patterns and associated mathematics for
closed-end air column. An instrument consisting of a closed-end column
typically contains a metal tube in which one of the ends is covered and not
open to the surrounding air. Some pipe organs and the air column within the
bottle of a pop-bottle orchestra are examples of closed-end instruments. Some
instruments that operate as open-end air columns can be transformed into
closed-end air columns by covering the end opposite the mouthpiece with a mute.
As we will see the presence of the closed end on such an air column will affect
the actual frequencies that the instrument can produce.
Standing
Wave Patterns for Harmonics
As has already been mentioned, a musical instrument has
a set of natural frequencies at which it vibrates at when a disturbance is
introduced into it. These natural frequencies are known as the harmonics of the
instrument. Each harmonic is associated with a standing wave pattern. In Lesson 4 of
Unit 10, a standing wave pattern was
defined as a vibrational pattern created within a medium when the vibrational
frequency of the source causes reflected waves from one end of the medium to interfere with
incident waves from the source in such a manner that specific points along the
medium appear to be standing still. In the case of stringed instruments
(discussed earlier), standing wave patterns were drawn to depict
the amount of movement of the string at various locations along its length.
Such patterns show nodes - points of no displacement or movement - at the two
fixed ends of the string. In the case of air columns, a closed end in a column
of air is analogous to the fixed end on a vibrating string. That is, at the
closed end of an air column, air is not free to undergo movement and thus is
forced into assuming the nodal positions of the standing wave pattern. Air at
the closed end of an air column is still. Conversely, air
is free to undergo its back-and-forth longitudinal vibration at the open end of
an air column. And as such, the standing wave patterns will depict vibrational
antinodes at the open ends of air columns.
So the basis for drawing the standing wave patterns for air
columns is that vibrational antinodes will be present at any open end and
vibrational nodes will be present at any closed end. If this principle is
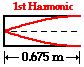
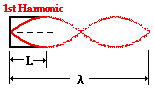
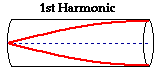
applied to closed-end air columns, then the pattern for the fundamental frequency
(the lowest frequency and longest wavelength pattern) will have a node at the
closed end and an antinode at the open end. For this reason, the standing wave
pattern for the fundamental frequency (or first harmonic) for a closed-end air
column looks like the diagram below.
The distance between adjacent antinodes on a standing wave pattern is
equivalent to one-half of a wavelength. Since nodes always
lie midway in between the antinodes, the distance between an antinode and a
node must be equivalent to one-fourth of a wavelength. A careful analysis of
the diagram above shows that a node and an adjacent antinode are positioned at
the two ends of the air column. Thus, the length of the air column is equal to
one-fourth of the wavelength for the first harmonic.
The fundamental frequency is the lowest possible frequency
that any instrument can play; it is sometimes referred to as the first harmonic
of the instrument. The second harmonic of any instrument always has a frequency
that is twice the frequency of the first harmonic. The fourth harmonic of any
instrument always has a frequency that is four times the frequency of the first
harmonic. As we will see, a strange pattern results for a closed-end air
column. Just as for all the instruments, the next harmonic for a closed-end air
column is the harmonic that has one more node. And just as for all the
instruments, the addition of an extra node also means that an extra antinode
must also be added to the pattern. This would result in a total of two vibrational antinodes
and one vibrational node. This pattern is shown in the diagram below.
Observe in the pattern that there is three-fourths of a full wave in the length
of the air column. That is three times the number of waves in the first
harmonic. Since, the frequency of this harmonic is three times the frequency of
the first harmonic, this is called the third harmonic.
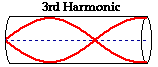
But what happened to the second harmonic? Unlike the other
instrument types, there is no second harmonic for a closed-end air column. The
next frequency above the fundamental frequency is the third harmonic (three
times the frequency of the fundamental). In fact, a closed-end instrument does
not possess any even-numbered harmonics. Only odd-numbered harmonics are
produced, where the frequency of each harmonic is some odd-numbered multiple of
the frequency of the first harmonic.
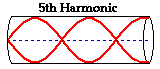
The next highest frequency above the third harmonic is the
fifth harmonic. It is the standing wave pattern with the next smallest
wavelength. The standing wave pattern for the fifth harmonic of a closed-end
air column is produced by adding another node to the pattern. This would result
in a total of three anti-nodes and three nodes. This pattern is shown in the
diagram below. Observe in the pattern that there are one and one-fourth waves
present in the length of the air column. That is five times the number of waves
in the first harmonic. For this reason, the frequency of the fifth harmonic is
five times the frequency of the first harmonic.
The process of adding another node and antinode to each
consecutive harmonic in order to determine the pattern and the resulting
length-wavelength relationship could be continued. If doing so, it is important
to keep vibrational antinodes on the open ends and vibrational nodes on the
closed end of the air column and to maintain an alternating pattern of nodes
and antinodes. When finished, the results should be consistent with the
information in the table below.
Length-Wavelength Relatiionships
The relationships between the standing wave pattern for a
given harmonic and the length-wavelength relationships for closed-end air
columns are summarized below.
|
Harmonic # |
# of Waves |
# of Nodes |
# of Antinodes |
Length- Wavelength Relationship |
|
|
1/4 |
1 |
1 |
λ = (4/1)*L |
|
|
3/4 |
2 |
2 |
λ = (4/3)*L |
|
|
5/4 |
3 |
3 |
λ = (4/5)*L |
|
|
7/4 |
4 |
4 |
λ = (4/7)*L |
|
|
9/4 |
5 |
5 |
λ = (4/9)*L |
(The symbol λ represents the wavelength.)
Problem-Solving
Scheme
Now the aim of the above discussion is to internalize the
mathematical relationships for closed-end air columns in order to perform
calculations predicting the length of air column required to produce a given
natural frequency. And conversely, calculations can be performed to predict the
natural frequencies produced by a known length of air column. Each of these
calculations requires knowledge of the speed of a wave in air (which is
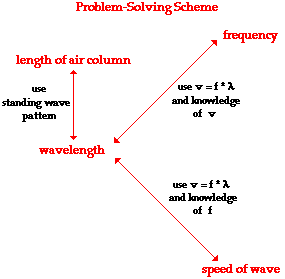
approximately 340 m/s at room temperatures). The graphic below depicts the relationships
between the key variables in such calculations. These relationships will be
used to assist in the solution to problems involving standing waves in musical
instruments.
To demonstrate the use of the above problem-solving scheme,
consider the following example problem and its detailed solution.
Example Problem #1
The speed of sound waves in air is 340
m/s. Determine the fundamental frequency (1st harmonic) of a closed-end air
column that has a length of 67.5 cm. |
The solution to the problem begins by first identifying known
information, listing the desired quantity, and constructing a diagram of the
situation.
|
Given: v = 340 m/s L = 67.5 cm = 0.675 m |
Find: f1 = ?? |
Diagram:
|
The problem statement asks us to determine the frequency (f)
value. From the graphic above, the only means of finding the frequency is to use the
wave equation (speed=frequency • wavelength) and knowledge of the speed and
wavelength. The speed is given, but wavelength is not known. If the wavelength
could be found then the frequency could be easily calculated. In this problem
(and any problem), knowledge of the length and the harmonic number allows one
to determine the wavelength of the wave. For the first harmonic, the wavelength
is four times the length. This relationship is derived from the diagram of the
standing wave pattern (see table above). The relationship, which works only for
the first harmonic of a closed-end air column, is used to calculate the
wavelength for this standing wave.
Wavelength = 4 • Length
Wavelength = 4 • 0.675 m
Wavelength = 2.7 m
Now that wavelength is known, it can be combined with the
given value of the speed to calculate the frequency of the first harmonic for
this closed-end air column. This calculation is shown below.
speed = frequency • wavelength
frequency = speed /
wavelength
frequency = (340 m/s) /
(2.7 m)
frequency = 126 Hz
Most problems can be solved in a similar manner. It is always
wise to take the extra time needed to set the problem up; take the time to
write down the given information and the requested information, and to draw a
meaningful diagram.
Seldom in physics are two problems identical. The tendency to
treat every problem the same way is perhaps one of the quickest paths to
failure. It is much better to combine good problem-solving skills (part of
which involves the discipline to set the problem up) with a solid grasp of the
relationships among variables. Avoid the tendency to memorize approaches to
different types of problems.
To further demonstrate the use of the above
problem-solving scheme, consider the following example problem and its detailed
solution.
Example Problem #2
Determine the length of an closed-end air column that produces a fundamental
frequency (1st harmonic) of 480 Hz. The speed of waves in air is known to be
340 m/s. |
The solution to the problem begins by first identifying known
information, listing the desired quantity, and constructing a diagram of the
situation.
|
Given: v = 340 m/s f1 = 480 Hz |
Find: L = ?? |
Diagram:
|
The problem statement asks us to determine the length of the
air column. From the graphic above, the only means of finding the
length of the air column is from knowledge of the wavelength. But the
wavelength is not known. However, the frequency and speed are given, so one can
use the wave equation (speed = frequency • wavelength) and knowledge of the
speed and frequency to determine the wavelength. This calculation is shown
below.
speed = frequency • wavelength
wavelength = speed
/ frequency
wavelength = (340
m/s) / (480 Hz)
wavelength = 0.708 m
Now that the wavelength is found, the length of the air
column can be calculated. For the first harmonic, the length is one-fourth the
wavelength. This relationship is derived from the diagram of the standing wave
pattern (see table above); it may also be evident to you by looking at the
standing wave diagram drawn above. This relationship between wavelength and
length, which works only for the first harmonic of a closed-end air column, is
used to calculate the wavelength for this standing wave.
Length = (1/4) • Wavelength
Length = (1/4) • Wavelength
Length = 0.177 m
If you have successfully followed the logic of the two
solutions above, then take a try at the following practice problems. As you
proceed, be sure to be mindful of the numerical relationships involved in such
problems. And if necessary, refer to the problem solving
scheme presented above.
Check Your Understanding
1. Titan Tommy and the Test Tubes at a night club this
weekend. The lead instrumentalist uses a test tube (closed-end air column) with
a 17.2 cm air column. The speed of sound in the test tube is 340 m/sec. Find the frequency of the first harmonic played by this
instrument.

Answer: 494 Hz
Given:
v = 340 m/s
L = 17.2 cm =
0.172 m (use meters for length since the speed is given in units of meters/s)
The strategy for solving for the frequency of the first harmonic
involves using the wave equation: v = f • λ where λ is the wavelength
of the first harmonic. Since the wavelength is not stated, it will have to be
calculated from the knowledge of the length of the closed-end air column. For
the first harmonic, the wavelength is four times the length of the air column
(see Tutorial page).
λ = 4 • L =
4 • (0.172 m) = 0.688 m
Now rearrange the wave equation v = f • λ to solve for
frequency.
f1 =
v / λ = (340 m/s) / (0.688 m) = 494 Hz
2. A closed-end organ pipe is used to produce a mixture of
sounds. The third and fifth harmonics in the mixture have frequencies of 1100
Hz and 1833 Hz respectively. What is the frequency of the first harmonic played
by the organ pipe?

Answer: 367 Hz
Given:
f = 1100 Hz (3rd
Harmonic)
f = 1833 Hz (5th
Harmonic)
The frequencies of the various harmonics of a closed end air
column are whole-number multiples of the frequency of the first harmonic. Each
harmonic frequency (fn) is given by the equation fn = n • f1 where n is the harmonic
number and f1 is the frequency of the first harmonic. Rearranging this
equation leads to f1 = fn /
n. So using the fifth harmonic frequency (f5) or the third harmonic
frequency (f3), the first harmonic frequency can be calculated.
f1 =
(1100 Hz) / 3 or (1833 Hz) / 5 = 367 Hz
3. Pipin' Pete is playing at
City Park next weekend. One of the closed-end pipes is capable of sounding out
a first harmonic of 349.2 Hz. The speed of sound in the pipe is 350
m/sec. Find the length of the air column
inside the pipe.

Answer: 0.250 m
Given: f = 349.2 Hz (1st H)
v = 350 m/s
The length of a closed-end air column is related mathematically
to the wavelength of the wave which resonates within it. Thus the strategy for
solving for length will be to first determine the wavelength of the wave using
the wave equation and the knowledge of the frequency and the speed. The wave
equation states that v = f •λ where λ is the wavelength of the wave.
Rearranging this equation and substituting allows one to determine the
wavelength.
λ = v / f =
(350 m/s) / (349.2 Hz) = 1.00 m
For the first harmonic, the length of a closed-end air column is
one-fourth the wavelength of the wave (see Tutorial page). Thus, the following
calculation can be performed:
L = 0.25 •
λ = 0.250
m